7. 분할 정복

7.1 도입

분할 정복(Divide & Conquer) 는 각개 격파 라고 간단히 설명 할 수 있다.
분할 정복이 일반적인 재귀 호출과 다른 점은 문제를 한 조각과 나머지 전체로 나누는 대신, 거의 같은 크기의 부분 문제로 나누는 것이다.
일반적인 재귀: 한 조각과 나머지로 쪼갬
분할 정복: 항상 절반씩 쪼갬

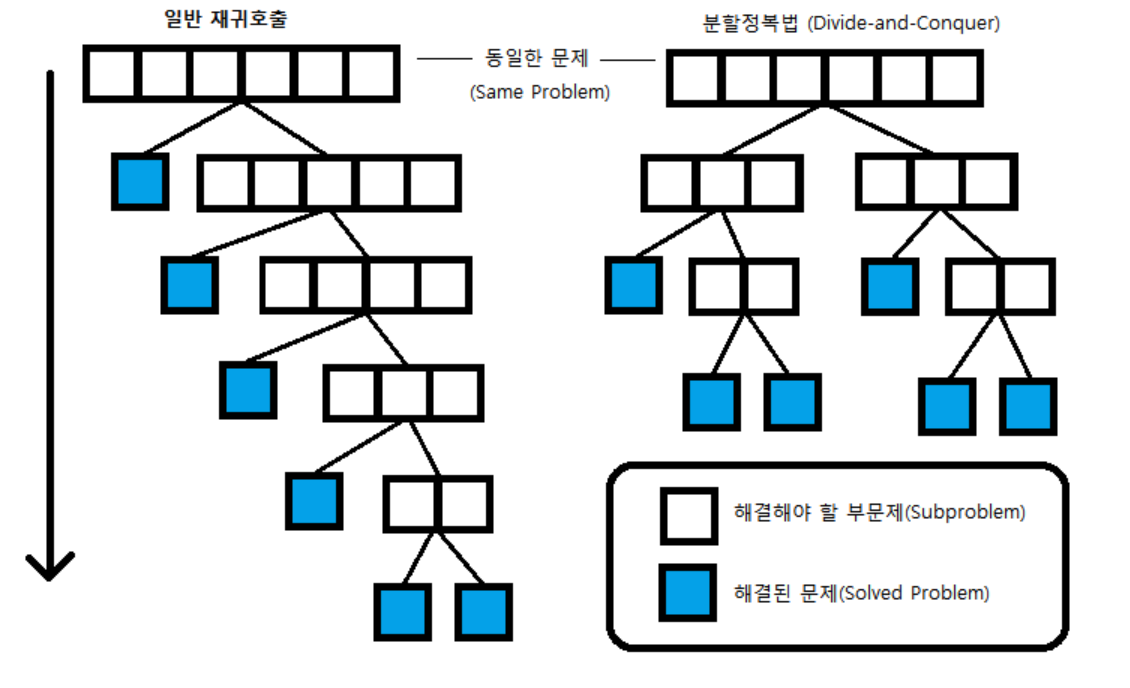
SCR-20240930-rlzw

분할 정복의 구성 요소
- divide(분할) : 문제를 더 작은 문제로 분할하는 과정
- merge(병합) : 각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정
- base case : 더 이상 답을 분할하지 않고 곧장 풀 수 있는 매우 작은 문제
분할 정복 문제의 특성
- 문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있어야 한다.
- 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 한다.
같은 문제라도 어떻게 분할하느랴에 따라 시간 복잡도 차이가 커진다.
절반으로 나누는 알고리즘이 큰 효율 저하를 불러오는 이유는 바로 여러 번 중복되어 계산되면서 시간을 소모하는 부분 문제들이 있기 때문이다.
- 이런 속성을 부분 문제가 중복된다(overlapping subproblems) 라고 한다.
- 이런 속성이 동적 계획법이 고안된 계기다.

두 개의 정렬 모두, 분할 정복 패러다임 기반
두 개의 정렬 모두 같은 아이디어로 정렬하지만, 시간이 많이 걸리는 작업을 분할(퀵 정렬), 에서 하느냐, 병합(병합 정렬) 단계
병합 정렬은 주어진 수열을 가운데에서 쪼개 비슷한 수열 두 개로 만든 뒤 이들을 재휘 호출을 이용해 각각 정렬한다.
그 후 정렬된 배열을 하나로 합침으로써 정렬된 전체 수열을 얻는다.
병합 정렬은 분할(divide)에는 O(1) 시간이 걸리고, 정렬된 배열들을 하나의 배열로 합치기 위해서 별도의 병합(merge) 과정에서 O(n) 시간이 걸린다.
퀵 정렬은 배열을 단순하게 가운데에서 쪼개는 대신, 병합 과정이 필요 없도록 한쪽의 배열에 포함된 수가 다른 쪽 배열의 수보다 항상 작도록 배열을 분할한다.
이를 위해, 파티션(paritition, 분할) 이라고 부르는 단계를 도입한다.
이는 배열에 있는 수 중 임의의 ‘기준 수(pivot)’ 를 지정한 후, 기준 보다 작거나 같은 숫자를 왼쪽, 더 큰 숫자를 오른쪽으로 보내는 과정이다.
분할에 O(n) 시간이 걸리고, 이미 정렬된 상태이기에, 별도의 병합 작업에 걸리는 시간이 거의 없다.

우리가 선택할 수 있는 접근 방법, 둘 중 어느 것이 맞는지 판단하기는 쉽지 않음, 보통 쉬운 것은 2번
1. 큰 입력에 대해서 동작하는 효율적인 알고리즘을 처음부터 새로 만들기
2. 작은 입력에 대해서만 동작하는 단순한 알고리즘으로 시작해서 최적화 해 나가기
압축 문자열 분할하기
- 각 부분의 길이가 일정하지 않기 때문에, 4 부분으로 쪼개기 쉽지 않음
- s를 미리 쪼개는 것이 아니라, ‘필요한 만큼 가져다 쓰도록’ 한다.
- s를 통째로 전달하는 것이 아니라, s의 한 글자를 가리키는 포인터를 전달하고, 한 글자씩 검사할때 마다, 이 포인터를 앞으로 한 칸씩 옮긴다.
압축 다 풀지 않고 뒤집기
- 2^20 x 2^20을 모두 저장하는 것은 현실적으로 불가능
- 압축을 해제한 결과를 메모리에 다 저장하는 대신 결과 이미지를 뒤집은 결과를 곧장 생성하는 코드를 작성하자.
1. 전체가 검은색이나 흰색인 그림은 뒤집어 봤자 다를게 없다. (base case)
2. 전체가 한 가지색이 아닌 경우에는 재귀 호출을 이용해 네 부분을 각각 상하로 뒤집은 결과를 얻은 뒤, 이들을 병합해 답을 얻는다.
- 1 -> 2 -> 3-> 4-> // 3 -> 4 -> 1 -> 2