8. 동적 계획법

8.1 도입

  • 동적 계획법(dynamic programming) 은 최적화 문제를 연구하는 수학 이론에서 왔으며,

    • 우리가 전산학 전반에서 사용하는 동적(dynamic), 프로그래밍이란 단어와는 관련이 없다.

  • 따라서, 바른 명명은 동적 프로그래밍이 아니라, 동적 계획법이다.

8.1.1 중복되는 부분 문제

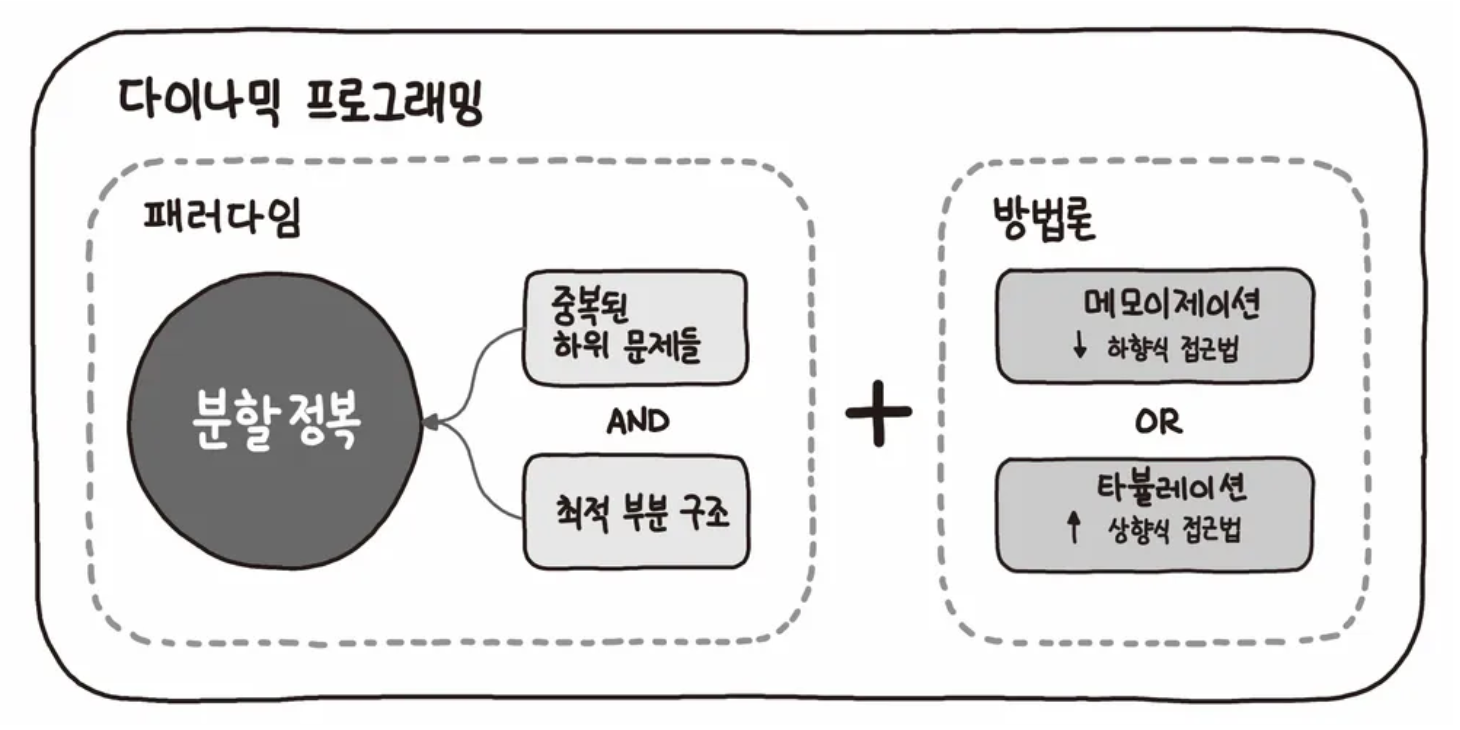
  • 동적 계획법은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다.

    • 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 내기 때문이다.
    • 동적계획법은 ‘어떤 부분 문제’를 ‘두 개 이상의 문제’를 푸는데 사용될 수 있기 때문에,
      • 이 문제의 답을 여러 번 계산하는 대신 한 번만 계산하고 계산 결과를 재활용 함으로써 속도의 향상을 꾀할 수 있다.
    • 이를 위해, 각 문제의 답을 메모리에 저장할 필요가 있고, 이 메모리 저장 장소를 cache(캐시) 라고 한다. => 메모이제이션, 캐싱
    • 두 번 이산 계산되는 부분 문제를 중복되는 부분 문제(overlapping subproblems) 라고 한다.

  • 분할 정복: 단순한 재귀 호출을 통해, 문제를 분할해도 한 부분 문제를 한 번만 해결

    • 계산의 중복 횟수는 분할의 깊이가 깊어질수록 지수적으로 증가, 이를 해결하기 위해 고안된 알고리즘이 동적 계획법

image-20240502094604917.png

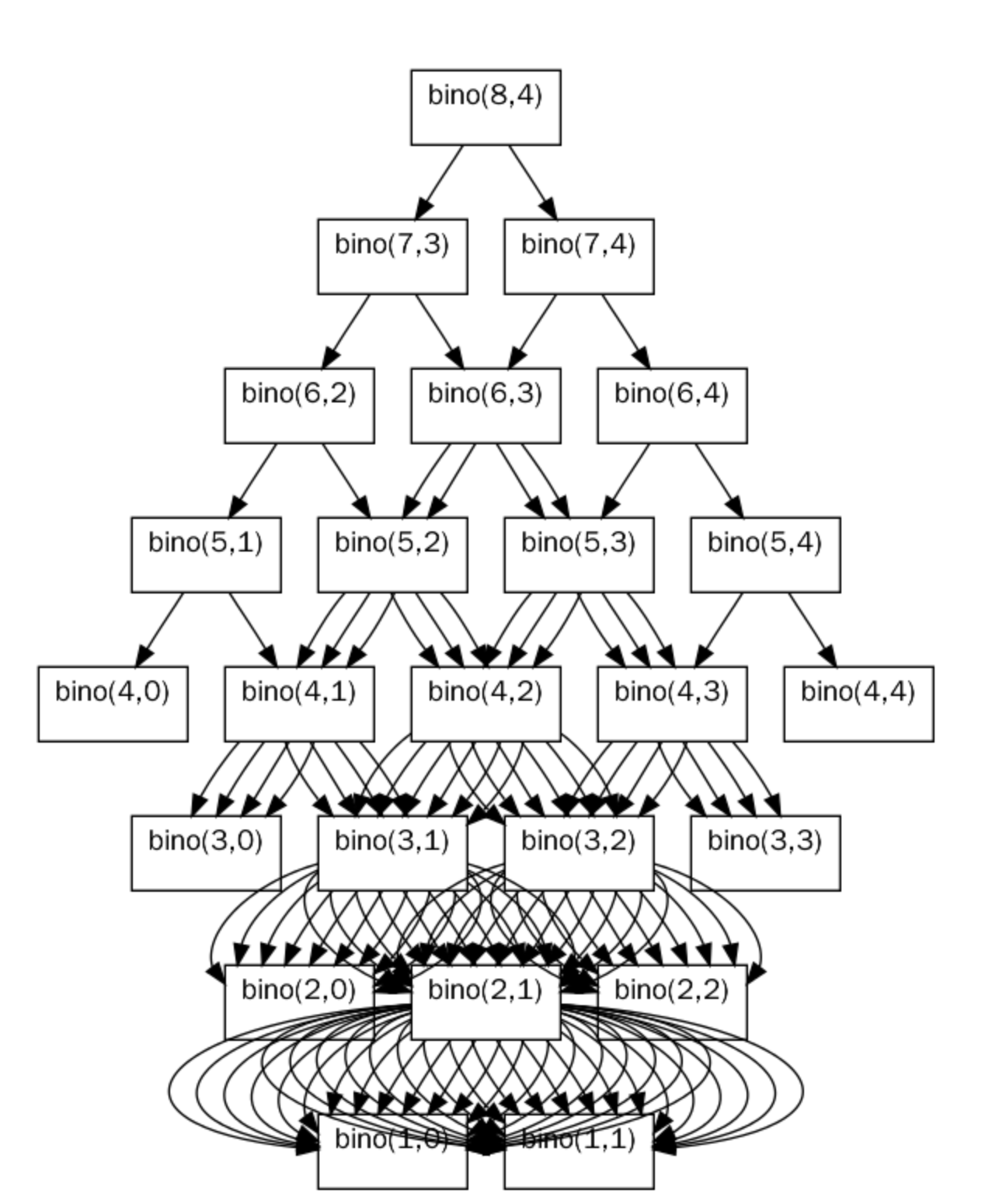
image-20240502094510502.png

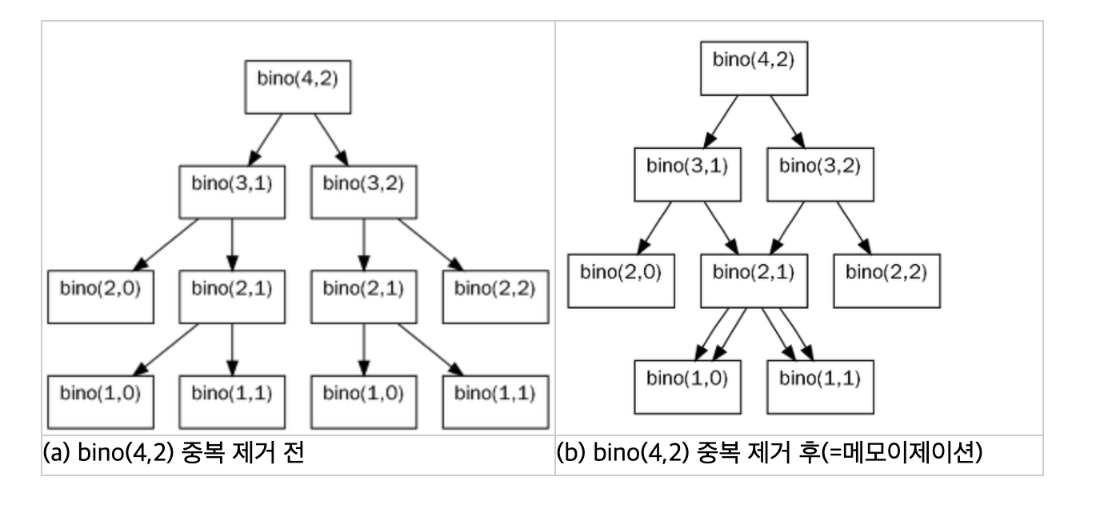
SCR-20240930-rmml

  • 몇몇 부분 문제 들은 여러 번 계산하기 됨
    • 캐시 배열을 만들어서, 각 배열에 저장되어 있는지 확인하고, 저장 되어 있다면 즉시 반환
    • 메모이제이션(memoization): 함수의 결과를 저장하는 장소를 마련해 두고, 한 번 계산한 값을 저장해 뒀다 재활용하는 최적화 기법
    • 메모이제이션을 사용하면 모든 부분 문제가 한 번씩만 계산된다고 보장할 수 있기 때문에 함수 호출 횟수가 엄청나게 감소한다.
  • 동적 계획법: 이와 같이 두 번 이상 반복되는 계산되는 부분 문제들의 답을 미리 저장함으로써, 속도의 향상을 꾀하는 알고리즘 설계 기법

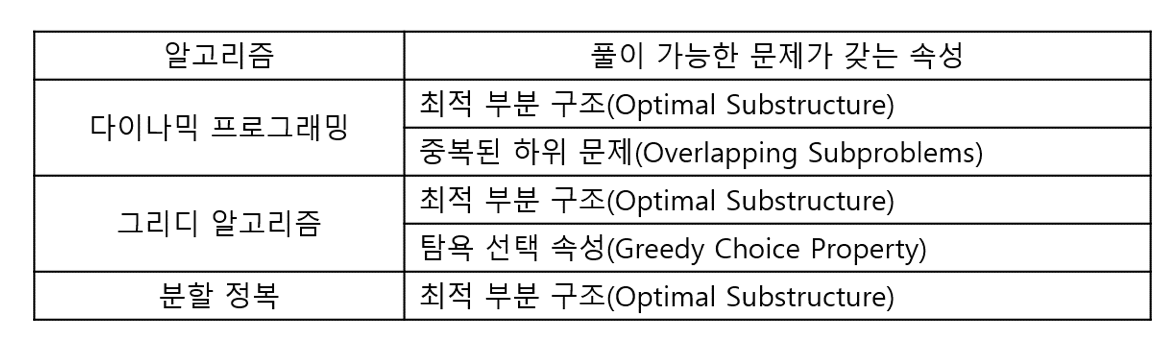
SCR-20240930-rmnb

8.1.2 메모제이션 구현 패턴

  • 항상 base case(기저 사례) 를 먼저 처리
  • cache 에 데이터가 저장되어 있으면 (답을 계산한 적이 있으면) 바로 반환

8.1.2 메모제이션의 시간 복잡도 분석

  • (주먹구구) 시간 복잡도: 존재하는 부분 문제의 수 x 한 부분 문제를 풀때 필요한 반복문의 수행횟수
    • 상한을 간단히 계산할 수 있는 방법, 항상 정확하지는 않음
    • 실제 수행 시간이 이 식 보다 더 간단할 수 있다.

8.1.3 동적 계획법 레시피

  1. 동적 계획법 알고리즘 만드는 첫 단계는 해당 문제를 재귀적으로 해결하는 완전 탐색 알고리즘을 만드는 것 부터 시작

  2. 중복된 부분 문제를 한 번 만 계산하도록 메모제이션을 적용

  • “원하는 답이 존재하는가?” 이 질문을 완전 탐색을 구할 때 흔히 가장 문제가 되는 것은, 원하는 답은 없는데 전체 답의 개수는 무지막지하게 많은 경우이다.
  • 완전 탐색의 경우, 어떤 경로는 마지막 칸에 도달할지도 모른다고 생각하고, 수없이 많은 경로를 일일히 탐색하게 된다. 경로의 갯수가 n에 대해 지수적 증가하게 됨

8.2, 8.3 와일드카드, WILDCARD, 난이도: 중

  • 비둘기 집 원리에 따라, 101 x 101 = 10201 번 이상 호출되었다면, 부분 문제가 존재할 수 밖에 없음.
  • 101 x 101 배열에 모든 부분 문제의 답을 저장 할 수 있음

8.4 전통적 최적화 문제들

  • 동적 계획법의 가장 일반적인 사용처는 최적화 문제 이다.

  • 최적화 문제: 여러 개의 가능한 답 중 가장 좋은 답(최적해) 를 찾는 문제

  • 최적화 문제에 특정 성질이 성립할 경우, 단순히 메모이제이션을 적용하는 것 보다 더 효율적으로 동적 계획법을 구현할 수 있다.

  • 예제) 삼각형 위의 최대 경로, TRIANGLEPATH, 난이도: 하

    • path1(y, x, sum) = 현재 위치가 (y, x)이고, 지금까지 만난 수의 합이 sum 일 때, 이 경로를 맨 아래줄까지 연장해서 얻을 수 있는 최대 합을 반환
    • 함수의 반환 값을 전체 경로의 최대치(path1)가 아니라, (y, x)에서 시작하는 부분 경로의 최대치로 바꾸면, 부분 문제들을 얻을 수 있다.
    • path2(y, x) = (y, x)에서 시작해서 맨 아래줄까지 내려가는 부분 경로의 최대 합을 반환

8.4.1 최적 부분 구조

  • 삼각형 위의 최대 경로 의 속도를 최적화 할 수 있는 sum이라는 정보가 (y, x) 에서 맨 아래줄까지 내려가는 문제를 해결하는 데 아무 상관이 없다 는 것 때문이다.
  • 어떤 경로로 이 부분 문제에 도달 했건, 남은 부분 문제는 항상 최적으로 풀어도 상관 없다는 의미이다,
    • 이 조건은 최적 부분 구조(optimal substruture) 라는 동적 계획법의 중요 요소 이다.
  • 최적 부분 구조(optimal substruture) 는 어떤 문제와 분할 방식에 성립하는 조건이다.
    • 각 부분 문제의 최적해만 있으면, 전체 문제의 최적해를 얻어 낼 수 있는 경우
    • 지금까지의 선택과 상관 없이, 각 부분 문제를 최적으로 풀기만 하면 전체 문제의 최적해도 알 수 있다는 것
  • 최단 경로 문제는 각 부분의 최적해가 전체의 최적해(최단 경로) 이기 때문에 최적 부분 구조를 갖는다.

8.4.2 최적화 문제, 동적 계획법 레시피

  1. 모든 답을 만들어 보고, 그 중 최적해의 점수를 반환하는 완전 탐색 알고리즘을 설계한다.
  2. 전체 답의 점수를 반환하는 것이 아니라, 남은 선택들에 해당하는 점수만을 반환하도록 부분 문제 정의를 바꾼다.
  3. 재귀 호출의 입력, 파라미터에 이전의 선택에 관한 정보가 있다면, 꼭 필요한 것만 남기고 줄인다.
  4. 문제에 최적 부분 구조가 성립할 경우, 이전 선택에 관련된 정보를 완전히 없앨 수 도 있다. 목표는 가능한 한 중복되는 부분 문제를 많이 만드는 것
  5. 입력의 종류가 줄어들면 줄어들 수 록, 더 많은 부분 문제가 중복되고, 메모이제이션을 최대한 활용할 수 있게 된다.
  6. 입력이 배열이거나 문자열인 경우, 적절한 변환을 통해 메모이제이션을 활용할 수 있도록 한다.
  7. 메모이제이션을 적용한다.

8.11 경우의 수와 확률

  • 동적 계획법은 경우의 수를 세거나 확률을 계산하는 문제에도 흔하게 사용된다.
    • 경우의 수를 새는 경우, 재귀적인 특징이 있기 때문이다.

8.11.1 타일링 방법의 수 세기, TILING2, 난이도: 하

  • 2 x n 사각형을 채우는 모든 방법들은 맨 왼쪽 세로줄이 어떻게 채워져 있느냐로 나눌 수 있다.
    • 이 두 가지 분류는 타일링 하는 방법을 모두 포함한다.
    • 두 가지 분류에 모두 포함되는 타일링 방법은 없다.
  • 결과적으로, 더 세지도 않고, 덜 세지도 않는다.
    • tiling(n) = tiling(n-1) + tiling(n-2) // 타일 1개 사용한 경우 + 타일 2개 사용한 경우

8.11.2 경우의 수, 계산하기 레시피

  1. 모든 답을 직접 만들어서 세어보는 완전 탐색 알고리즘을 설계한다.
    • 모든 경우는 이 선택지들에 포함됨 (덜 세지 않음)
    • 어떤 경우도 두 개 이상의 선택지에 포함되지 않음 (더 세지 않음)
  2. 최적화 문제를 해결할 때 처럼, 이전 조각에서 결정한 요소들에 대한 입력, 파라미터를 없애거나 변형해서 줄인다.
  3. 재귀 함수는 앞으로 남아 있는 조각들을 고르는 경우의 수만 반환해야 한다.
  4. 메모이제이션을 적용한다.

Reference