유명한 알고리즘이나 자료 구조를 도구로 사용해 풀어야 하는 문제들에 대해 다룸

13. 수치 해석

13.1 도입

• 수치 해석: 직접 풀기 힘든 수학 문제를 근사적으로 푸는 알고리즘과 오차의 범위, 수치적 안정성을 연구하는 전산학의 분야

13.2 이분법

• 이분법: 주어진 범위 [lo, hi] 내에서 어떤 함수 f(x)의 값이 0이 되는 지점을 수치적으로 찾아내는 기법
  • 이분법은 이분탐색의 토대가 된다.
• 정해진 횟수만큼 반복하기
  • 반복문을 100번 반복하면, 절대 오차가 최대 lo-hi / 2 ^101 이 된다.
  • 이 오차는 10 ^ -7 보다 작다. 따라서 큰 숫자를 다루는 경우에도 충분히 답을 구할 수 있다.

14. 정수론

14.1 소수 판별

• O( √N ) 소수 판별 알고리즘 (다른 알고리즘 보다 빠르다.)

  • num이 합성 수 이면, p x q 꼴로 나타내어지고, p는 항상 √Num 이하, q는 항상 √Num 이상 이다.
  • 따라서, num-1 까지 순회하지 않고, √Num 까지만 순회

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  def isPrime1(n): if n <= 1: return False if n == 2: return True if (n % 2) == 0: return False sqrtn = sqrt(n) for div in range(3, sprt + 1, 2): if (n % div) == 0: return False def isPrime2(n): end = int(n**(1/2)) for i in range(2, end+1): if n % i == 0: return False return True

14.2 에라토스테네스의 체

• 주어진 수 Num 이하의 소수들을 모두 찾아낸다. (배열로 return이 가능)

• n 까지의 수를 배열로 만든 상태에서 시작

• 시간 복잡도: O(NloglogN) // 실용적인 범위에서 O(N)와 거의 비슷

• 시간 보다는 메모리 사용량이 관건이다.

  1 2 3 4 5 6 7 8 9 10

  def getPrimeNumbers(num): # by 에라토스테네스의 체 arr = [i for i in range(num + 1)] # 인덱싱을 수월하게 하기 위해 0부터 배열 선언 end = int(num ** (1 / 2)) for i in range(2, end + 1): if arr[i] == 0: # 이미 소수가 아님이 판별된 수는 건너뜀 continue for j in range(i * i, num + 1, i): # 자기 자신을 제외한 i의 배수는 모두 0으로 처리함. arr[j] = 0 return [i for i in arr[2:] if arr[i]]

14.5 유클리드 알고리즘

• 최대 공약수를 구하는 알고리즘
• 두 수, p, q (p > q)의 공약수의 집합은 p - q와 q의 공약수 집합과 같다는 점을 이용
• gcd(q, p) = gcd(p-q, q)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def gcd(a, b): # 재귀 
    if a % b == 0:
        return b
    return gcd(b, a % b)

def gcd(a, b): # 반복문
    while b > 0:
        a, b = b, a % b
    return a

def lcd(a, b):
    return a * b // gcd(a, b)

14.8 모듈러 연산

• 모듈러 연산: 모듈러(modulus) M에 도달하면 다시, 0으로 돌아가는 정수들을 가지고 하는 연산이다.

  • Ex) 시계는 25시나 42시가 없다, 1시나, 18시로 표현해야 한다.
    • 시간(hour): 0~23 / M = 24

• a % b 는 a 를 b로 나눈 나머지를 의미한다. (%: 나머지 연산자)

• 두 수를 더한 뒤 나머지를 취하는 것은 미리 두 수의 나머지를 구한 뒤 더하고, 다시 나머지를 취하는 것과 같다.

  • 덧셈, 곱셈, 뺄셈에 적용, 나눗셈은 적용 안됨

15. 계산 기하

15.1 다각형 면적 구하기

1
2
3
4
5
6

figure.append(figure[0])
area = 0
for i in range(N):
    area += figure[i][0]*figure[i+1][1] - figure[i+1][0]*figure[i][1]
    
area = area / 2

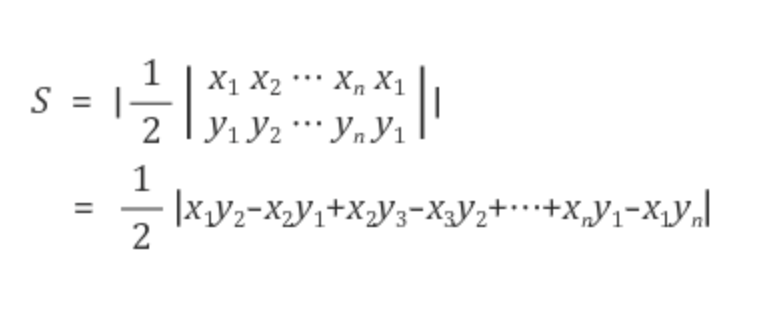
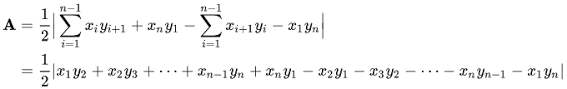
15.2 스위핑 알고리즘

• 평면 스위핑(Plane Wweeping), 라인 스위핑(Line Sweeping)이라고 불리는 패턴이 있습니다.

• 평면 스위핑을 이용하는 알고리즘들은 수평선 혹은 수직선으로 주어진 평면을 ‘쓸고 지나가면서’ 문제를 해결합니다.

• 스위핑 알고리즘이란 단어의 뜻 그대로 휩쓸고 지나가며 문제를 해결하는 방식으로,

• 특정 기준에 따라 정렬한 후 순서대로 처리하는 알고리즘이다.

  • 보통 문제들의 경우 인풋의 범위만큼 브루트 포스를 사용하게 되면 선분일 경우 N의 시간복잡도 이다. 평면: N^2

  • 스위핑 알고리즘은 정렬의 시간복잡도인 NlogN이 대부분이다.

투 포인터

투 포인터의 기본 개념

• 포인터: 배열이나 리스트의 특정 인덱스를 가리키는 변수입니다.

• 투 포인터: 두 개의 포인터를 사용하여 배열의 양쪽 끝이나, 두 위치에서 출발하여 동시에 배열을 탐색하는 방식입니다.

• Python 예시 코드

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  n = 5 # 데이터의 개수 N m = 5 # 찾고자 하는 부분합 M data = [1,2,3,2,5] count = 0 interval_sum = 0 end = 0 for start in range(n): # start를 차례대로 증가시키며 반복 while interval_sum < m and end < n: # end를 가능한 만큼 이동시키기 interval_sum += data[end] end += 1 if interval_sum == m: # 부분합이 m일 때 카운트 증가 count += 1 # start 가 증가 되기 때문에 (맨 위 for문) data[start] 값 만큼 빼주어야 한다. interval_sum -= data[start]

투 포인터의 동작 원리

• 두 개의 포인터를 배열이나 리스트의 다른 위치에 두고, 각 포인터를 조절하면서 문제를 해결합니다.
• 주로 하나의 포인터가 시작점을 가리키고, 다른 포인터가 끝점 또는 그 외의 적절한 지점을 가리킵니다.
• 각 포인터는 문제 조건에 맞게 이동하며 탐색 범위를 좁혀 나가거나 넓혀 나갑니다.

투 포인터의 사용 사례

(1) 정렬된 배열에서 두 수의 합을 구하는 문제 (Two Sum Problem)

• 배열에서 두 숫자의 합이 특정 값이 되는 쌍을 찾는 문제.

• 동작 방식:

  1. 배열이 정렬되어 있는 상태에서, 하나의 포인터는 시작 지점(왼쪽 끝), 다른 포인터는 끝 지점(오른쪽 끝) 에서 시작합니다.
  2. 두 수의 합이 목표 값보다 작으면 왼쪽 포인터를 오른쪽으로 이동시킵니다(값을 크게 하기 위해).
  3. 두 수의 합이 목표 값보다 크면 오른쪽 포인터를 왼쪽으로 이동시킵니다(값을 작게 하기 위해).
  4. 두 포인터가 만날 때까지 이 과정을 반복하며, 목표 값을 찾습니다.

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  fun twoSum(arr: IntArray, target: Int): Pair<Int, Int>? { var left = 0 var right = arr.size - 1 while (left < right) { val sum = arr[left] + arr[right] if (sum == target) { return Pair(left, right) // 두 수의 인덱스를 반환 } else if (sum < target) { left++ // 합이 작으면 왼쪽 포인터를 오른쪽으로 } else { right-- // 합이 크면 오른쪽 포인터를 왼쪽으로 } } return null // 목표 값에 맞는 두 수를 찾지 못함 } fun main() { val arr = intArrayOf(1, 2, 3, 4, 6) val target = 6 val result = twoSum(arr, target) println(result) // 출력: (1, 3), 즉 arr[1] + arr[3] = 2 + 4 = 6 }

(2) 부분 배열의 합 문제 (Subarray Sum Problem)

• 배열에서 연속된 부분 배열의 합이 특정 값이 되는 경우를 찾는 문제.
• 동작 방식:
  1. 하나의 포인터는 부분 배열의 시작점, 다른 포인터는 부분 배열의 끝점을 가리킵니다.
  2. 부분 배열의 합이 목표 값보다 작으면 끝 포인터를 오른쪽으로 이동시켜 배열을 확장하고, 합이 목표 값보다 크면 시작 포인터를 오른쪽으로 이동시켜 배열을 축소합니다.

(3) 두 배열 병합 (Merging Two Sorted Arrays)

• 정렬된 두 배열을 하나의 배열로 합치는 문제.

• 동작 방식:

  1. 각 배열에 하나씩 포인터를 두고, 각 배열의 포인터가 가리키는 값을 비교하면서 작은 값을 결과 배열에 추가합니다.
  2. 한 배열의 모든 요소가 처리될 때까지 이 과정을 반복합니다.

(4) 세 수의 합 문제 (Three Sum Problem)

• 배열에서 세 수의 합이 특정 값이 되는 세 숫자를 찾는 문제.
• 해결 방법:
  • 첫 번째 수는 배열을 순회하면서 선택하고, 나머지 두 수의 합을 찾는 부분은 투 포인터 알고리즘을 사용하여 해결합니다.
  • 예시 코드 (세 수의 합 문제는 중복 처리와 관련된 추가적인 로직이 필요합니다).

백준 30804번 문제: 과일 탕후루

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

from collections import defaultdict

n = int(input())
arr = list(map(int, input().split()))
ans, dic, left = 0, defaultdict(int), 0

for right in range(n):
    dic[arr[right]] += 1

    while len(dic) > 2:
        dic[arr[left]] -= 1
        if dic[arr[left]] == 0:
            del dic[arr[left]]

        left += 1
        
    ans = max(ans, right - left + 1)

print(ans)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

def addDict(num):
    if num in dic: dic[num] += 1
    else: dic[num] = 1

def minusDict(num):
    if dic[num] == 1: del dic[num]
    else: dic[num] -= 1

n = int(input())
arr = list(map(int, input().split()))
if n == 1 or n == 2:
    print(n)
    exit()

ans, l, r, dic = 2, 0, 1, dict()
addDict(arr[l])
addDict(arr[r])

while l < n and r < n:
    if len(dic) <= 2:
        ans = max(ans, r - l + 1)
        if r + 1 < n:
            r += 1
            addDict(arr[r])
        else:
            break
    else:
        minusDict(arr[l])
        l += 1

print(ans)

투 포인터의 복잡도

• 메모리 사용량이 적습니다. 추가적인 메모리 공간을 거의 사용하지 않으며, 대부분의 경우 상수 공간 복잡도(O(1)) 를 유지합니다.

• 투 포인터(Two Pointers) 알고리즘의 시간 복잡도는 일반적으로 O(N) 입니다. 이는 대부분의 투 포인터 문제에서, 배열이나 문자열을 한 번만 순회하기 때문입니다.

투 포인터의 시간 복잡도 분석

• 기본 원리: 투 포인터 알고리즘은 보통 배열의 양 끝 또는 특정 위치에서 두 개의 포인터를 설정하고, 각 포인터가 배열을 한 방향으로 이동합니다.

  • 두 포인터는 서로를 향해, 또는 같은 방향으로 이동하면서 배열을 한 번에 한 요소씩 처리합니다.

  • 포인터들이 한 번에 하나의 요소만 스캔하기 때문에 전체 배열을 한 번만 순회하게 됩니다.

• 상세 분석: 배열이나 문자열의 길이를 N이라고 할 때

  • 각 포인터는 배열의 한 끝에서 시작해서, 배열의 다른 끝까지 한 번만 이동합니다.

  • 두 포인터의 움직임이 반복될 때, 한 번의 움직임은 배열의 한 요소만을 처리하므로, 각 포인터는 최대 N번의 연산을 수행하게 됩니다.

정렬된 배열에서 두 수의 합 찾기

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

fun twoSum(arr: IntArray, target: Int): Pair<Int, Int>? {
    var left = 0
    var right = arr.size - 1

    while (left < right) {
        val sum = arr[left] + arr[right]

        if (sum == target) {
            return Pair(left, right)
        } else if (sum < target) {
            left++
        } else {
            right--
        }
    }
    return null
}

• left 포인터는 시작점에서 오른쪽으로 이동하고, right 포인터는 끝점에서 왼쪽으로 이동합니다.
• 각 포인터가 배열을 최대 한 번씩만 이동하므로, 시간 복잡도는 O(N) 입니다.

부분 배열의 합 구하기

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

fun subarraySum(arr: IntArray, target: Int): Pair<Int, Int>? {
    var currentSum = 0
    var start = 0

    for (end in arr.indices) {
        currentSum += arr[end]

        while (currentSum > target && start <= end) {
            currentSum -= arr[start]
            start++
        }

        if (currentSum == target) {
            return Pair(start, end)
        }
    }

    return null
}

• end 포인터는 배열을 순차적으로 탐색하면서 오른쪽으로 이동합니다.
• start 포인터는 필요할 때만 오른쪽으로 이동합니다.
• 여기서도 start와 end 모두 배열의 각 요소를 최대 한 번씩만 방문하므로, 시간 복잡도는 O(N) 입니다.

투 포인터가 유용한 상황

• 정렬된 배열이나 리스트에서 특정 조건을 만족하는 쌍을 찾거나, 부분 배열을 탐색할 때.

• 연속된 부분 배열 또는 서로 다른 배열을 동시에 탐색해야 하는 문제.

• 배열의 양쪽 끝에서부터 범위를 줄여가며 최적의 해를 구해야 할 때.

Slow-Fast 알고리즘

• Slow-Fast 알고리즘(또는 토끼와 거북이 알고리즘, Floyd’s Tortoise and Hare Algorithm)은 연결 리스트나 배열에서 두 개의 포인터를 사용하는 기법입니다.
• 두 포인터를 서로 다른 속도로 움직여 문제를 해결하는 방식으로, 특히 순환이 있는지 또는 사이클을 탐지하는 문제에서 자주 사용됩니다.
• 시간 복잡도는 일반적으로 O(N), 공간 복잡도는 O(1) 로 매우 효율적입니다.

개념

• Slow 포인터는 한 번에 한 칸씩 이동하고,
• Fast 포인터는 한 번에 두 칸씩 이동합니다.
• 두 포인터가 이동하다가 같은 지점에 도달하면, 그 구조에는 순환(사이클)이 존재한다는 것을 의미합니다. 반대로, Fast 포인터가 끝에 도달하면 순환이 없다는 것을 알 수 있습니다.

활용 사례

• 연결 리스트에서 사이클 탐지
• 중간 노드 찾기
• 사이클 시작 지점 찾기

대표적인 문제들

연결 리스트에서 사이클 탐지

주어진 연결 리스트가 순환(Cycle) 이 있는지 여부를 판별하는 문제입니다.

1. Slow 포인터는 한 번에 한 칸씩 이동하고,
2. Fast 포인터는 한 번에 두 칸씩 이동합니다.
3. 두 포인터가 어느 순간 만나면 순환이 있다는 것을 의미합니다.
4. 만약 Fast 포인터가 끝까지 도달하면 순환이 없다는 뜻입니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class ListNode(val value: Int) {
    var next: ListNode? = null
}

fun hasCycle(head: ListNode?): Boolean {
    var slow = head
    var fast = head

    while (fast?.next != null) {
        slow = slow?.next          // 한 칸 이동
        fast = fast.next?.next     // 두 칸 이동

        if (slow == fast) {
            return true  // 두 포인터가 만나면 순환이 있음
        }
    }

    return false  // fast가 끝에 도달하면 순환이 없음
}

사이클의 시작 지점 찾기

연결 리스트에 사이클이 존재하는 경우, 그 사이클의 시작 지점을 찾아내는 문제입니다.

1. 사이클을 감지하기 위해 Slow-Fast 알고리즘을 먼저 사용합니다.
2. 두 포인터가 만나면, Slow 포인터를 다시 리스트의 시작 지점으로 이동시킵니다.
3. 그 후 Slow 포인터와 Fast 포인터를 각각 한 칸씩 이동시키면, 두 포인터는 사이클의 시작 지점에서 만나게 됩니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

fun detectCycle(head: ListNode?): ListNode? {
    var slow = head
    var fast = head

    // 사이클 존재 여부 확인
    while (fast?.next != null) {
        slow = slow?.next
        fast = fast.next?.next

        if (slow == fast) {
            // 사이클 발견 시, slow를 시작점으로 이동
            var cycleStart = head
            while (cycleStart != slow) {
                cycleStart = cycleStart?.next
                slow = slow?.next
            }
            return cycleStart  // 사이클 시작 지점 반환
        }
    }

    return null  // 사이클이 없는 경우 null 반환
}

배열에서 중복 요소 찾기

배열에서 1부터 N까지의 숫자가 들어있을 때, 하나의 숫자가 중복되어 들어있는 배열이 있다고 가정합니다. 이때 중복된 숫자를 찾아내는 문제입니다.

중복된 숫자는 사이클을 형성하는 것으로 간주할 수 있으며, 이를 찾는 방식은 연결 리스트의 사이클 탐지와 유사합니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

fun findDuplicate(nums: IntArray): Int {
    var slow = nums[0]
    var fast = nums[0]

    // 사이클 존재 여부 확인
    do {
        slow = nums[slow]
        fast = nums[nums[fast]]
    } while (slow != fast)

    // 사이클 시작 지점 찾기
    var finder = nums[0]
    while (finder != slow) {
        finder = nums[finder]
        slow = nums[slow]
    }

    return finder  // 중복된 숫자 반환
}

Reference

• 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 (구종만, 인사이트)
• https://www.algospot.com/