17. 부분 합, 누적 합, 구간 합

17.1 도입

  • 누적 합(Cumulative Sum, prefix sum): 배열의 각 위치에 대해 배열의 시작부터 현재 위치까지의 원소의 합을 미리 구해 둔 배열
    • O(N), 수열의 길이에 선형으로 증가
  • 누적 합(Cumulative Sum)을 미리 구해 두면, list의 특정 구간의 합(range sum)을 O(1)에 구할 수 있다.
    • cumulativeSum[-1] = 0이라 가정할 때, list[a]부터 list[b]까지의 합은 cumulativeSum[b] - cumulativeSum[a-1] 이다.
  • 핵심: O(N) 시간으로 계산한 누적 합을 통해서, 구간 합을 O(1) 시간으로 빠르기 구하기
  • 누적 합(Cumulative Sum) 은 첫 위치가 항상 A[0]으로 고정된, 구간 합(range sum) 이라고 할 수도 있다.
  • 부분 합은 Partial Sum 이라 한다. 수열의 어느 부분의 합을 의미한다.

17.1.2 2차원으로의 확장

  • 누적 합은 2차원 배열에서 A[y1, x1]에서 A[y2, x2]까지의 직사각형 구간의 합을 계산해야 할 때도 유용하다.

  • cumulativeSum[y, x]는 (0, 0)을 왼쪽 위 칸, (y, x)를 오른쪽 아래 칸으로 갖는 직사각형 구간에 포함된 원소들의 합

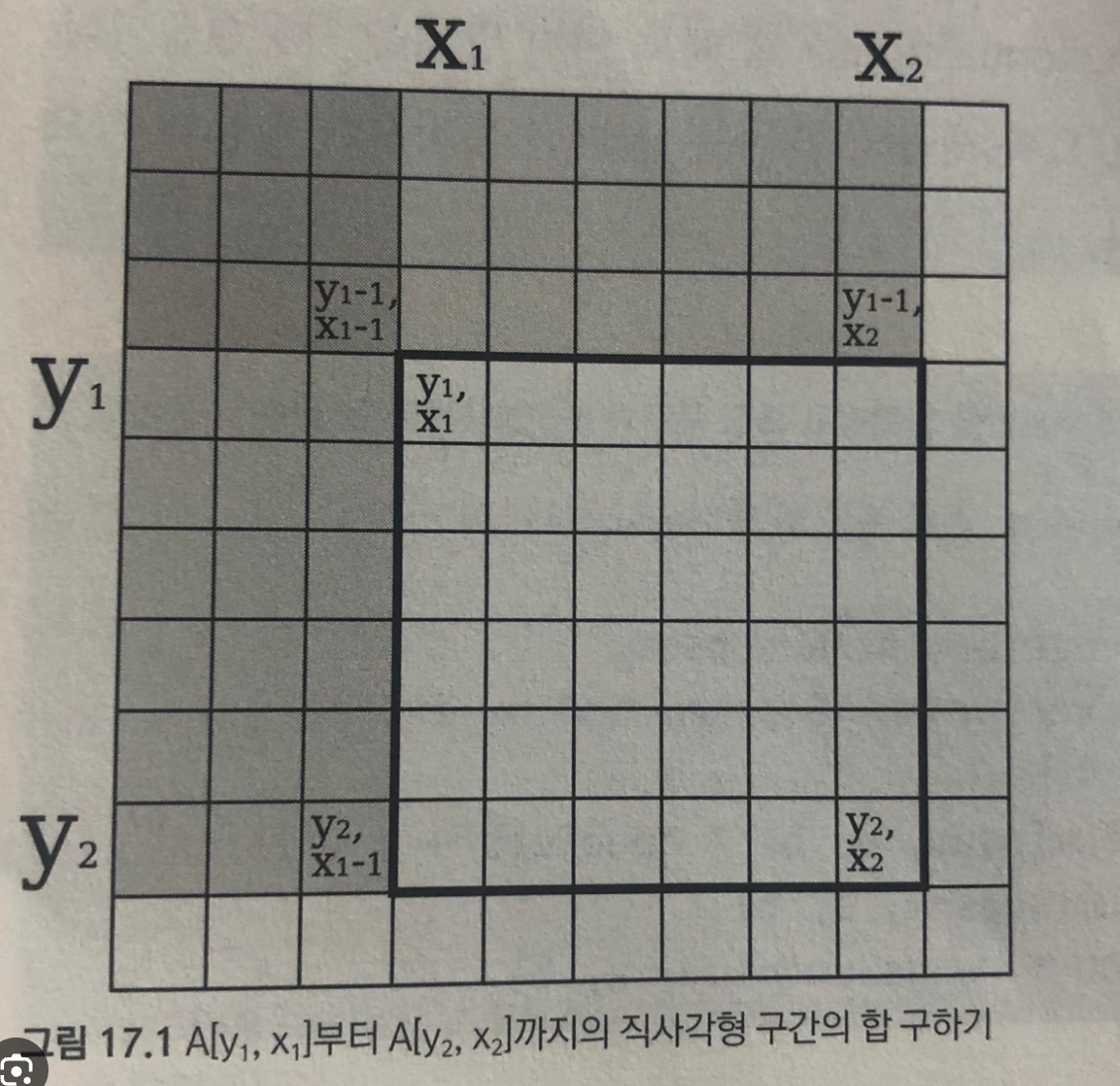
    image-20240327204330937.png

  • 누적 합을 이용한 구간 합 구하기

    • 그림에서 굵은 선으로 표시된 구간의 합(range sum)
    • sum(y1, x1, y2, x2) = cumulativeSum[y2, x2] - cumulativeSum[y2, x1 - 1] - cumulativeSum[y1 - 1, x2] + cumulativeSum[y1 - 1, x1 - 1]

17.1.3 예제: 합이 0에 가장 가까운 구간

  • 0 에 가장 가깝다는 말: cumulativeSum[ ]의 두 값의 차이가 가장 적다는 말

    • 완전 탐색: O(N^2)

    • 누적 합 이용

      • 정렬: O(NlogN)

      • 얻은 누적 합을 이용해서, 인접한 원소들 확인하는 것: O(N)

      • 총 결과: O(NlogN)

  • 배열에서 가장 가까운 두 값을 찾기 위한 방법

    • 이 배열을 정렬한 뒤, 인접한 원소들끼리 확인
    • Ex) 9, 100, 101, 300, 308 => (100, 101)

17.2 누적 합(Cumulative Sum), 구간 합(range Sum) 코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

lst = [3, 5, 7, 9]
N = len(lst)
cumulativeSum = [0] 

for i in range(0, N):  # 누적 합 구하기
    cumulativeSum.append(cumulativeSum[i] + lst[i])  # [0, 3, 8, 15, 24]

# 0 <= leftIdx < rightIdx < N
def calRangeSum(lIdx, rIdx): # leftIdx 부터 rightIdx 까지의 합
    global cumulativeSum
    return cumulativeSum[rIdx + 1] - cumulativeSum[lIdx]

print(calRangeSum(0, 0)) # 3
print(calRangeSum(0, 1)) # 8
print(calRangeSum(0, 3)) # 24
print(calRangeSum(2, 3)) # 12
print(calRangeSum(3, 3)) # 9

  • 초기에, cumulativeSum = [0] 으로 초기화 해야, 이후 계산이 편해진다.

    • ‘cumulativeSum[-1] = 0이라 가정’ 에 해당

  • 실제 PS에 누적 합 알고리즘을 쓸 때, 구간 인덱스가 0 or 1부터 인지 꼭 확인해야 한다.

  • 이 코드는 idx를 기준으로 계산하는 코드이다.

    • 0 <= leftIdx < rightIdx < N

  • 일반적인 구간 합 레퍼런스는 범위 정수를 기준으로 알려져 있다.

    • 이 경우에는 calRangeSum(left, right) = cumulativeSum[right - 1] - cumulativeSum[left] 이다.

슬라이딩 윈도우 (Sliding Window)

슬라이딩 윈도우는 고정된 크기의 범위(윈도우) 를 데이터를 순차적으로 이동시키면서, 일정한 구간의 데이터를 효율적으로 처리하는 알고리즘 기법입니다.

이 방식은 특히 연속적인 구간에서 합계나 최대값, 최소값 등을 구하는 문제에서 자주 사용됩니다.

핵심 아이디어

슬라이딩 윈도우는 전체 데이터를 처리하지 않고, 고정된 크기의 구간을 한 칸씩 이동하면서 그때그때 구간 내의 값을 업데이트하는 방식입니다.

구간을 이동할 때, 이전 구간의 값을 활용하여 새로운 구간의 계산을 빠르게 처리할 수 있습니다.

슬라이딩 윈도우의 활용 상황

  1. 연속된 구간의 합을 구하는 문제
  2. 최대/최소값을 구하는 문제
  3. 부분 배열/문자열의 패턴 매칭 문제

슬라이딩 윈도우의 기본 예시: 연속된 구간의 합을 구하는 문제

예를 들어, 배열에서 크기 k인 구간의 합을 구하는 경우를 생각해보세요. 배열이 [1, 3, 2, 6, 4, 5, 8]이고, k = 3이라면 크기 3인 구간의 합을 차례로 구하고 싶습니다.

1. Naive 접근법 (비효율적)

모든 구간을 하나씩 새로 계산하는 방법은 다음과 같습니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

public class Main {
    public static void main(String[] args) {
        int[] arr = {1, 3, 2, 6, 4, 5, 8};
        int k = 3;

        // 각 구간의 합을 계산 (구간의 시작 인덱스는 i)
        for (int i = 0; i <= arr.length - k; i++) {
            int sum = 0;
            for (int j = i; j < i + k; j++) {
                sum += arr[j];
            }
            System.out.println("Sum of window starting at " + i + ": " + sum);
        }
    }
}
  • 여기서는 각 구간의 합을 구할 때마다 모든 원소를 다시 더하고 있습니다. 이 방법은 시간 복잡도가 O(n*k) 이므로 비효율적입니다.

2. 슬라이딩 윈도우를 이용한 효율적인 방법:

한 번 계산한 구간에서, 구간을 한 칸 오른쪽으로 이동할 때 맨 앞의 값을 빼고, 새로 추가되는 값을 더하는 방식으로 합을 계산하면, 중복 계산을 피할 수 있습니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

fun main() {
    val arr = arrayOf(1, 3, 2, 6, 4, 5, 8)
    val k = 3

    // 초기 구간의 합 계산
    var sum = 0
    for (i in 0 until k) {
        sum += arr[i]
    }
    println("Initial sum: $sum")

    // 슬라이딩 윈도우로 구간을 한 칸씩 이동하면서 합을 업데이트
    for (i in 1..arr.size - k) {
        sum = sum - arr[i - 1] + arr[i + k - 1]
        println("Sum of window starting at $i: $sum")
    }
}

Initial sum: 6
Sum of window starting at 1: 11
Sum of window starting at 2: 12
Sum of window starting at 3: 15
Sum of window starting at 4: 17

슬라이딩 윈도우 활용법:

  • 초기 윈도우 구간을 설정한 후, 구간이 이동할 때마다 이전 구간에서 제외되는 값을 빼고 새롭게 추가되는 값을 더하는 방식으로 계산을 빠르게 업데이트합니다.
  • 이렇게 하면 시간 복잡도가 O(n) 으로 줄어들어, 더 큰 데이터를 효율적으로 처리할 수 있습니다.

활용 예시 1: 최대 구간 합

배열에서 연속된 k개의 요소 중 최대 구간 합을 구하는 문제를 슬라이딩 윈도우로 해결할 수 있습니다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

fun main() {
    val arr = arrayOf(1, 3, 2, 6, 4, 5, 8)
    val k = 3

    // 초기 구간의 합 계산
    var maxSum = 0
    for (i in 0 until k) {
        maxSum += arr[i]
    }
    var currentSum = maxSum

    // 슬라이딩 윈도우로 구간을 한 칸씩 이동하면서 최대 구간 합 계산
    for (i in 1..arr.size - k) {
        currentSum = currentSum - arr[i - 1] + arr[i + k - 1]
        if (currentSum > maxSum) {
            maxSum = currentSum
        }
    }

    println("Maximum sum of any window: $maxSum")
}

활용 예시 2: 문자열에서 부분 문자열의 패턴 매칭

슬라이딩 윈도우는 문자열에서도 유용하게 쓰입니다. 예를 들어, 주어진 문자열에서 특정 길이의 부분 문자열이 패턴에 맞는지 확인하는 문제를 슬라이딩 윈도우로 해결할 수 있습니다.

슬라이딩 윈도우의 장점:

  1. 효율성: 슬라이딩 윈도우는 불필요한 반복 계산을 줄여, 처리 속도를 크게 향상시킵니다.
  2. 시간 복잡도: 많은 문제에서 슬라이딩 윈도우 기법을 사용하면, 전체 배열이나 문자열을 매번 새로 계산하는 대신, O(n) 복잡도로 문제를 해결할 수 있습니다.

시간 복잡도 분석

  1. 초기 구간 계산:

    • 슬라이딩 윈도우 기법에서는 먼저 첫 번째 구간에 대한 합을 계산합니다. 이 작업은 구간의 크기 k에 대해 O(k) 의 시간이 소요됩니다.
    1
2
3
4
5

    // 초기 구간의 합 계산 (O(k))
int sum = 0;
for (int i = 0; i < k; i++) {
    sum += arr[i];
}

  2. 구간 이동 및 업데이트:

    • 이후, 윈도우를 한 칸씩 이동하면서, 이전 구간의 맨 앞 값을 빼고, 새로운 값을 더하는 방식으로 구간 합을 업데이트합니다. 이 작업은 한 번의 이동당 O(1) 의 시간이 소요됩니다.
    1
2
3
4

    // 슬라이딩 윈도우로 구간을 한 칸씩 이동하면서 합을 업데이트 (O(n - k))
for (int i = 1; i <= arr.length - k; i++) {
    sum = sum - arr[i - 1] + arr[i + k - 1];
}

  3. 전체 배열을 처리:

    • 슬라이딩 윈도우는 배열을 한 번 순회하는 동안 고정된 크기의 구간을 이동하면서 계산을 수행합니다. 배열 전체의 크기가 n이라면, 전체 시간 복잡도는 O(n) 이 됩니다.

최종 시간 복잡도:

  • 초기 구간 계산: O(k) (구간의 크기 k만큼의 합을 처음에 계산)
  • 구간 이동 및 업데이트: O(n - k) (나머지 n - k개의 구간을 계산)
  • 전체 시간 복잡도: O(n)

즉, 슬라이딩 윈도우는 배열 전체를 한 번 순회하면서 각 구간을 효율적으로 계산하기 때문에, O(n) 의 시간 복잡도로 문제를 해결할 수 있습니다.

Reference