18. 선형 자료 구조

18.1 도입

  • 일렬로 늘어선 같은 종류의 자료 여러 개를 저장하기 위한 가장 기초적인 자료구조는 배열(Array) 이다.

  • 동적 배열, 연결 리스트는 배열과 비슷하지만, 배열에서 비효율적이거나 할 수 없는 작업들을 효율적으로 작업한다.

18.2 동적 배열

  • 배열(일반 배열, 정적 배열) 의 문제는 배열을 선언할 때, 배열의 크기를 지정해야 하며, 그 이상의 자료를 집어넣을 수 없다는 점이다.

  • 이 문제를 해결 하기 위해, 자료의 개수가 변함에 따라 크기가 변경되는 동적 배열(dynamic array)이 고안되었다.

  • 동적 배열은 또 다른 종류의 배열이 아니다.

  • 동적 배열은 일반 배열처럼 언어 차원에서 지원되는 기능이 아니다.

  • 동적 배열은 일반 배열을 이용해 만들어 낸 별도의 자료 구조 이다.

  • 동적 배열은 대개 언어 문법이 아니라 언어의 표준 라이브러리에 포함되어 있다.

  • 내부적으로는 일반 배열로 구현되기 때문에, 동적 배열은 일반 배열이 갖는 특성을 그대로 물려 받는다.

  • 요즘에는 일반적인 배열을 제공하지 않고 동적 배열만을 제공하는 언어들도 있다.
    • 동적 타입을 갖는 언어, 대표적으로 Python
  • 이 동적 배열 기능도 내부적으로는 항상 일반 배열로 구현된다.

18.2.1 일반 배열의 특성

  • 일반 배열은, 동적 배열과 비교하면 정적 배열로 볼 수 있다.
  • 원소들은 메모리의 연속된 위치에 저장된다.
    • 캐시의 효율성을 높여준다, 공간 지역성
  • 주어진 위치의 원소를 반환하거나 변경하는 동작을 O(1) 에 할 수 있다.
  • 배열에 원소를 삽입, 삭제
    • O(N), 원소를 삽입, 삭제하고 기존 원소를 모두 이동(데이터 복사)시켜줘야 한다.
    • 정확한 수행 시간은 삽입, 삭제의 위치에 따라 달라지지만, 평균적으로 선형 시간
  • 임의 접근(random access) 가 O(1) 에 가능하다.
    • 순차 접근과 달리 인덱스에 해당하는 데이터에 접근할 수 있다.

18.2.2 동적 배열의 특성

  • 일반 배열의 특성을 그대로 물려 받음
  • 컴파일 시점에 크기를 지정해야 하는 일반 배열의
  • 배열의 크기를 변경하는 resize() 연산이 가능
    • O(N) 시간이 걸림
  • 주어진 원소를 배열의 맨 끝에 추가함으로써, 크기를 1 늘리는 append() 연산을 지원한다.
    • O(1) 시간이 걸림

18.2.3 동적 배열의 연산

  • 동적 배열의 연산을 하기 위해서는 동적으로 할당받은 배열(dynamically allocated array)을 사용한다.
    • 동적으로 할당받은 배열은 new 등의 연산으로 고정된 길이의 배열
  • 동적 배열의 크기가 바뀌어야 할 때는 단순하게 새 배열을 동적으로 할당받은 뒤 기존 원소들을 복사하고, 새 배열을 참조하도록 바꿔치기 한다
  • 새 배열을 할당받고 기존 자료를 복사하는 데는 배열의 크기에 비례하는 시간이 걸린다.
    • 따라서, resize() 연산은 O(N)
1
2

val size: Int; // 현재 배열의 크기
val arrayPointer: ElemntType // (동적으로 할당 받은) 실제 배열을 가리키는 포인터

img.png

  • 메모리를 할당받을 때 배열의 크기가 커질 때를 대비해서 여유분의 메모리를 미리 할당받으면, append()를 O(1)에 구현할 수 있다.

    • 배열이 이미 할당한 메모리에 꽉 찼을 때, 더 큰 메모리를 할당받아 배열의 원소를 그 쪽으로 전부 옮긴다.

  • 배열의 용량(capacity): 할당 받은 메모리의 크기

  • 배열의 크기(size): 실제 원수의 수

  • 여유분의 메모리(capacity)가 있지만, 실제로 동적 배열을 사용하는 프로그램에서는 배열의 크기가 5이라고 인식

  • 만약 현재 배열의 크기가 용량보다 작다면 append() 연산은 size를 1 증가 하고, 그 위치에 새 값을 할당하는 것으로 O(1) 에 구현 가능

    1
2

    // append(newValue)의 일부
array[size++] = newValue

  • 미리 할당해 둔 메모리가 꽉 찼을 때 append()는 어떻게 되는가?

    • 재할당: 더 큰 새 배열을 동적으로 할당받고, 새 배열에 기존 배열의 내용을 모두 복사한 다음 배열에 대한 포인터를 바꿔치기 한다.
    • 미리 정해좋은 M이라는 크기만큼 배열의 용량을 늘려준다고 할 때, 시간 복잡도는 O(N+M), 선형 시간, 매우 가끔 일어남
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// 배열 용량이 꽉 찼으면 재할당받는다.
if (size == capacity) {
    int newCapacity = capacity + M; // 정해진 값 M 만큼의 새로운 배열을 새로 할당한다.
    int* newArray = new int[newCapacity];

    for (int i = 0 ; i < size ; ++i)  // 기존 배열의 원소들을 복사한다.
    	newArray[i] = array[i];

    if (array) delete [] array;  // 기존 배열을 삭제한 뒤 , 새로운 배열로 바꿔치기 한다.
    array = newArray;
    capacity = newCapacity;
}

// size의 값을 1 늘리고, 새로운 값(newValue)를 추가한다.    
array[size++] = newValue;

18.2.4 동적 배열의 재할당 전략

  • 재할당에 걸리는 시간 복잡도 계산

    • 연산을 아주 여러 번 반복해서 수행한 뒤 각 수행 시간의 평균을 내자. // 분할 상환 분석(amortized analysis)
    • 각 재할당 과정에서 선형 시간이 걸리더라도, 그것이 아주 가끔 일어난다면 전체 평균은 여전히 상수 시간일 수 도 있다.

  • 텅 빈 배열로 시작해서, N번 append 연산을 할 때, 재할당의 수 K = O(N/M) 이다.

    • M은 상수이므로 N이 아주 커지면, K = O(N)
    • 재할당마다 복사하는 원소의 수는 M, 2M, 3M … KM개로 증가
    • 전체 복사하는 원소의 수는 (K+1)KM * 1/2 = O(K^2) = O(N^2)

  • N번의 append 연산에 드는 시간이 O(N^2) 이면, 한 번의 append 연산에 드는 시간은 평균적으로, O(N^2) / N = O(N) 이다.

    • 결과적으로 상수 시간에 append를 구현할 수 없게 된다.

  • 상수 시간 [ O(1) ] 에 append를 구현하는 비결

    • 재할당을 할 때마다 정해진 개수의 여유분을 확보하는 것이 아니라, 현재 가진 원소의 개수에 비례해서 여유분을 확보하는 것이다.

    • 예를 들어, 배열 용량이 부족할 때마다 용량을 두 배로 늘리는 방법, 1,2,4 …

      image-20240328202838810.png

  • 배열의 용량이 꽉 찼을 때 이것을 어떻게 증가, 또는 반대로 감소시키느냐의 전략은 동적 배열의 효율성에 큰 영향을 미친다.

18.2.5 표준 라이브러리의 동적 배열 구현

  • 현대에 사용되는 대부분의 언어들은 동적 배열을 표준 라이브러리에서 제공한다. C언어만 제외
    • C++: vector, Java: ArrayList , Kotlin: MutableList, Python: List
  • 이들은 내부적으로 배열(Array, 일반 정적 배열) 를 사용하기 때문에, 이들은 배열과 거의 다를 것 없는 속도를 제공한다.
  • 최종 크기가 얼마인지 알 수 있다면, 동적 배열의 용량을 미리 늘려둠으로써 재할당에 드는 비용을 줄이기
    • Java의 ArrayList에서 ensureCapacity() 를 호출 하면 된다.

18.3 연결 리스트

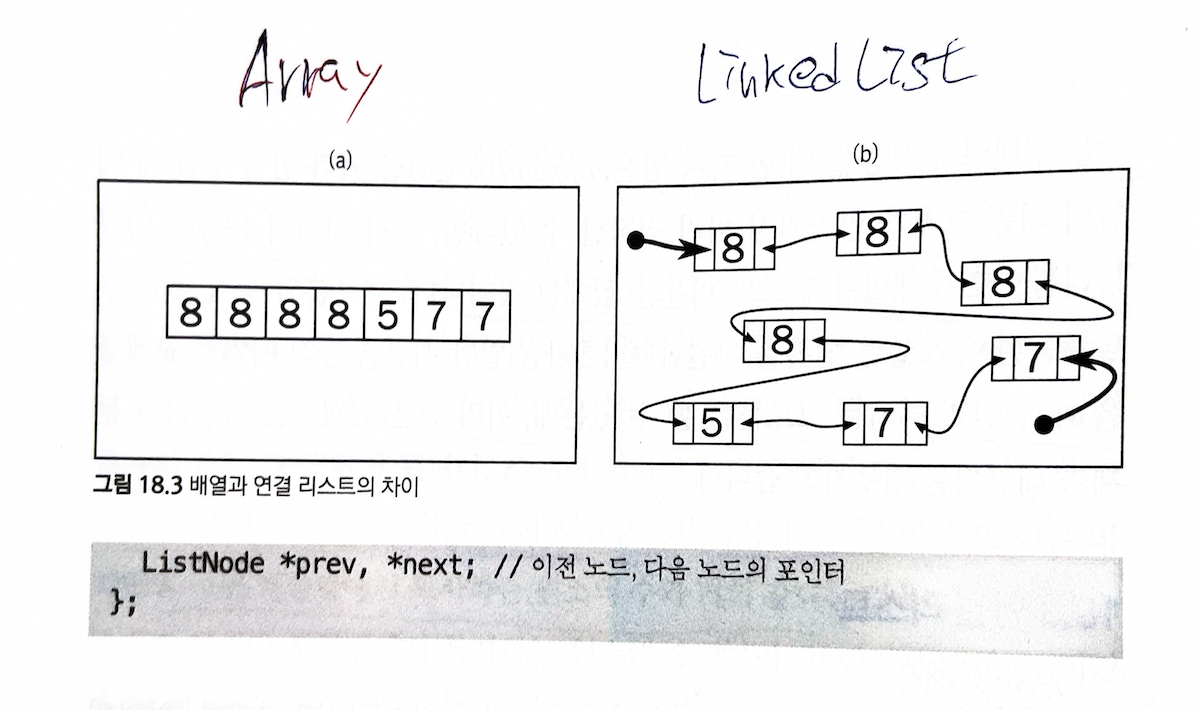
  • 배열과 달리, 메모리에 원소들이 물리적으로 흩어져 있고, 각 원소들이 이전과 다음 원소를 가리키는 포인터를 가지고 있다.

  • 데이터를 감싼 노드를 포인터로 연결해서 공간 효율성을 극대화 시킨 자료 구조

  • 삽입과 삭제를 상수 시간에 할 수 있게 해준다.

  • 이와 같은 연결 리스트를 정확히는 양방향 연결 리스트(doubly linked list) 라고 한다.

1

data class Node<T>(var element: T, var next: Node<T>? = null) 

1
2
3
4
5

class LinkedList<T> {
    private var head: Node<T>? = null
    private var tail: Node<T>? = null
	private var size = 0
}
  • 원소와 포인터들의 집합들을 리스트의 노드(node)라고 부른다.
  • 대게 연결 리스트는 head, tail에 대한 포인터만을 가진 클래스로 구현된다.

18.3.1 연결 리스트 특성

  • 특정 위치의 값을 찾기(탐색) 가 쉽지 않다.
    • i번째 노드를 찾 데 드는 시간은 리스트의 길이에 선형 비례 한다. O(N)
    • 연결 리스트의 머리부터 하나씩 포인터를 따라가며 다음 노드를 찾을 수 밖에 없다.
  • 삽입, 삭제
    • 노드들의 순서가 포인터에 의해 정의되기 때문에, 삽입, 삭제는 간단하다. O(1)
    • 다른 노드들은 그대로 두고, 삽입/삭제 노드와 이전/이후 노드의 포인터만을 바꾸면 된다.

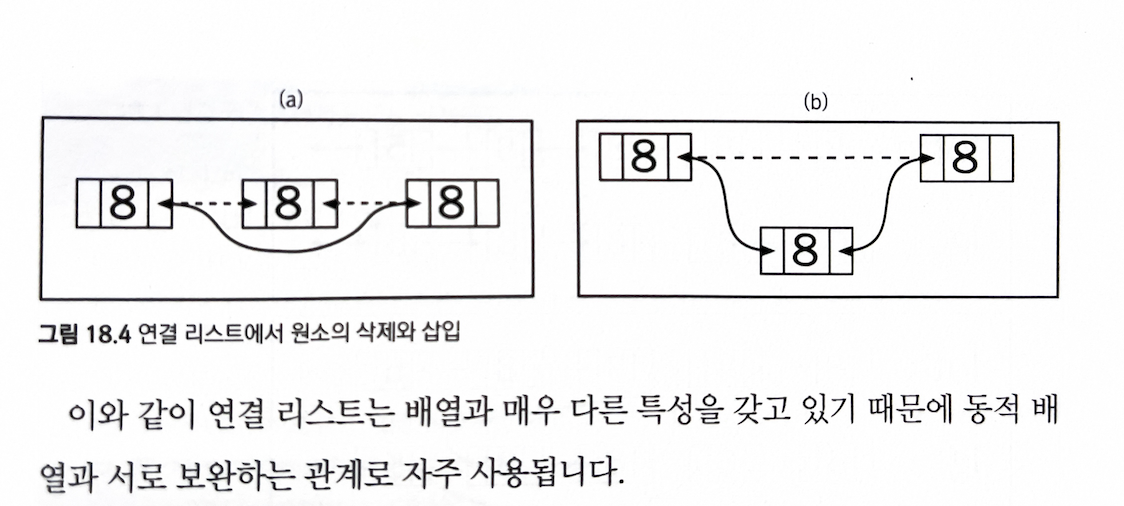
image-20240329113209558.png

18.3.2 표준 라이브러리의 연결 리스트 구현

  • 동적 배열과 같이, 대부분의 프로그래밍 언어에서 연결 리스트를 표준 라이브러리에서 제공한다.
    • C++ STL의 list, Java: LinkedList

18.3.3 연결 리스트 응용 연산들

  • splicing: 잘라 붙이기 연산

    • 다른 리스트를 통째로 삽입 하는 것을 상수 시간에 할 수 있다.
    • 잘라 붙이기 연산을 구현하면 연결 리스트의 크기를 O(1)에 알기 불가능해진다.
    • 연결 리스트의 크기를 알 수 있는 방법이 없어서, 원소의 개수를 리스트 객체에서 유지하면서 새 원소를 삽입하거나 삭제할 때마다 갱신해줘야 한다.
    • 하지만, 잘라 붙이기 연산을 할 때는 몇 개의 원소가 추가 되는지 알기 없기 때문이다.
    • 이 때문에 잘라 붙이기 연산을 지원하는 연결 리스트 구현은 많지 않다.
      • Java의 LinkedList의 구현은 잘라 붙이기 연산을 포기하는 대신, 리스트의 크기를 구하는 연산을 상수 시간에 지원한다.

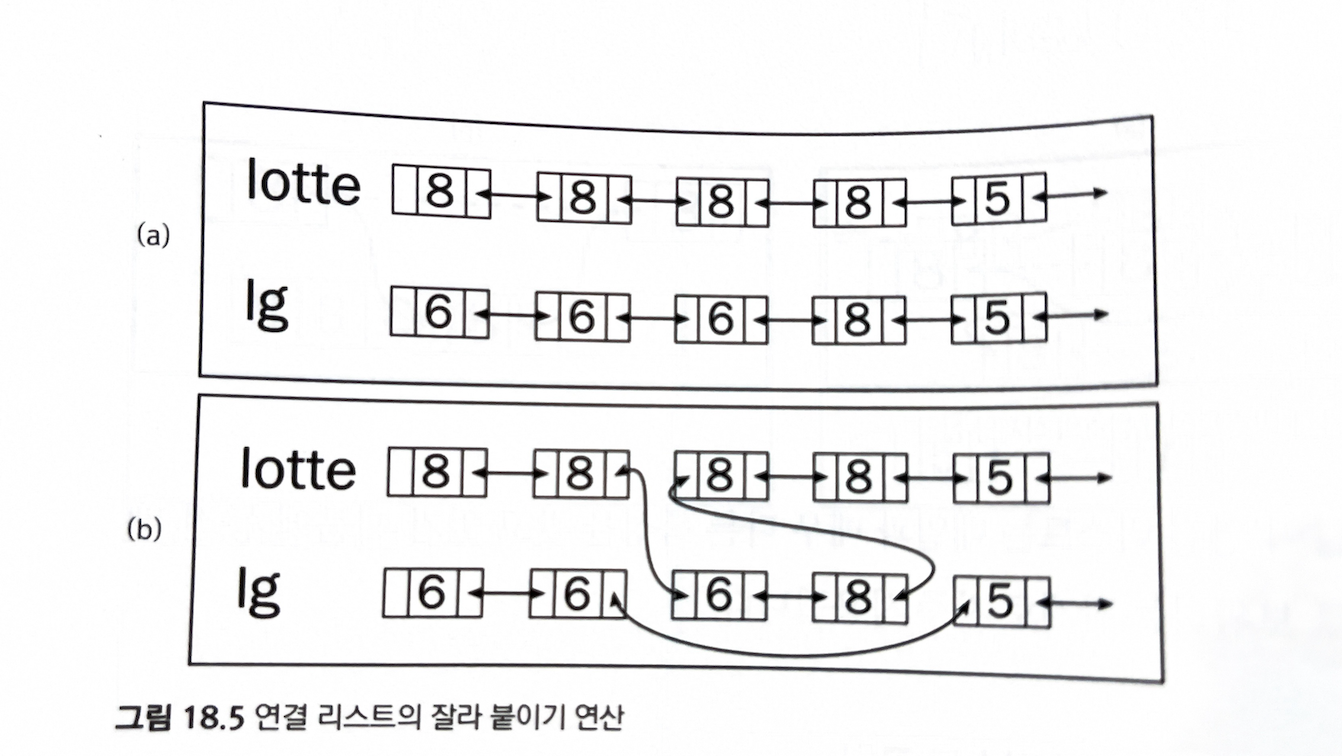
    image-20240329113327961.png

  • 삭제했던 원소 돌려놓기: 한 번 삭제했던 원소를 제자리에 쉽게 돌려 놓을 수 있다.

    • node의 포인터들은 원래 자기가 들어가 있던 위치를 알고 있기 때문에, recoverNode() 처럼 node에 대해서만 알고 있어도 원래 리스트에 쉽게 다시 삽입할 수 있다.

    • 이 방법은 이전, 이후 노드 또한 삭제된 상태에서 수행되면 리스트를 망가뜨리기 때문에, 항상 삭제한 순서의 반대로 복구가 이루어질 때만 사용할 수 있다.

    • 이 연산은 프로그램의 되돌리기(undo) 연산을 지원하는 데 유용하게 쓸 수 있다.

      • 사용자 인터페이스(UI)에 되돌리기 연산이 자주 사용

    • 양뱡향 연결 리스트로 문제의 현재 상태를 표현하면 되돌리기 연산을 통해 문제의 상태를 되돌리는 작업을 효율적으로 할 수 있다: 조합 탐색 에 유용하다.

       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

      // node 이전/이후 노드의 포인터를 바꿔서 node를 리스트에서 삭제한다
void deleteNode(listNode* node){
	node->prev->next = node->next;
    node->next->prev = node->prev;
}

// node 이전/이후 노드의 포인터를 바꿔서 자기 자신을 다시 리스트에 삽입
void recoverNode(listNode* node){
	node->prev->next = node;
    node->next->prev = node;
}

18.4 동적 배열과 연결 리스트 비교

  • 삽입, 삭제가 많다 => 연결 리스트

  • 원소 접근이 많다 => 동적 배열

  • 배열의 끝에서만 삽입, 삭제가 많다 => 동적 배열

    image-20240329113259570.png

    작업동적 배열연결 리스트
    이전 원소/다음 원소 찾기O(1)O(1)
    맨 뒤에 원소 추가/삭제하기O(1)O(1)
    맨 뒤 이외의 위치에 원소 추가/삭제하기O(N)O(1)
    임의의 위치의 원소 찾기O(1)O(N)
    크기 구하기O(1)O(N) or O(1), 잘라 붙이기 연산 유무에 따라

Reference