20. 문자열

20.1 도입

  • 현대의 컴퓨터는 많은 양의 문자열 자료를 다룬다.
  • 문자열 검색 문제를 위한 KMP 알고리즘
  • 문자열 처리를 위한 자료 구조, 접미사 배열(suffix array)
  • substring, 부분 문자열
  • prefix, 접두사
  • suffix, 접미사

20.2 문자열 검색

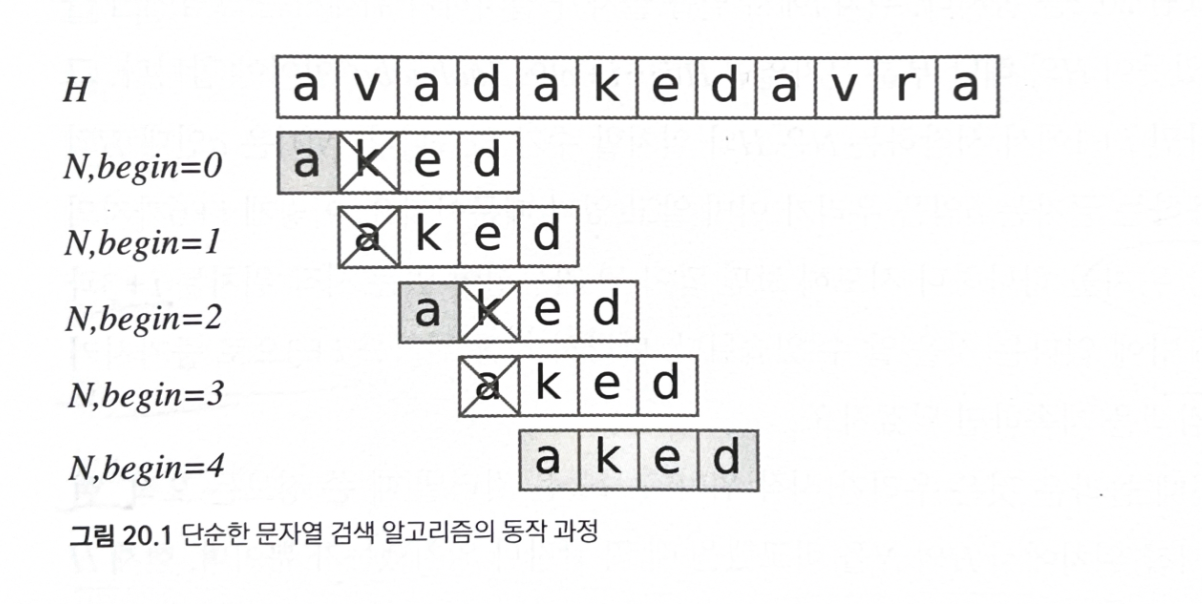
20.2.1 단순 문자열 검색 알고리즘

  • H, N 모두 a로만 구성된 긴 문자열이라면 H - N +1 개의 모든 시작 위치에 대해서 비교를 수행하게 된다.

  • 시작 위치의 수: O(H)

  • 각각의 비교: O(N)

  • 시간 복잡도: O(N*H)

    image-20240425142717243.png

20.2.2 KMP 알고리즘

image-20240425154620645.png

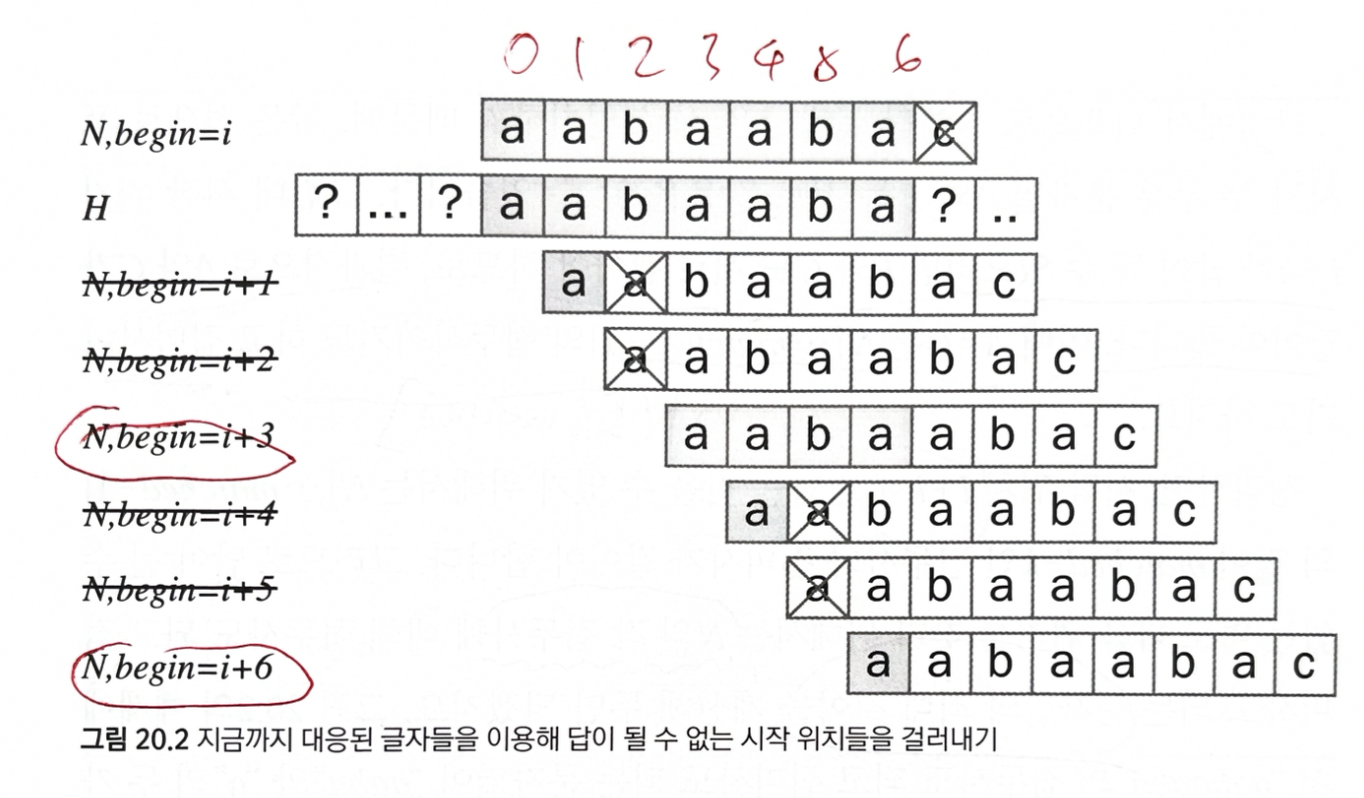
  • 긴 문자열에서 N = “aabaabac” 를 찾는 경우

  • 단순한 알고리즘은 i는 답이 아니니까, i+1에서 다시 답을 찾기 시작한다.

  • 시작 위치 중 일부는 답이 될 수 없음을 보지 않아도 알 수 있다.

  • 답이 될 수 있는 가능성이 있는, 시작 위치는 i+3과 i+6 밖에 없다.

  • 일치한 글자의 수는 항상 0 ~ N 사이의 정수

  • 전처리 과정에서 이 정보들을 미리 계산해 저장해 둘 수 있다.

  • 이러한 최적화 알고리즘이 Knuth-Morris-Pratt, KMP 알고리즘 이다.

image-20240425142735702.png

image-20240425154639901.png

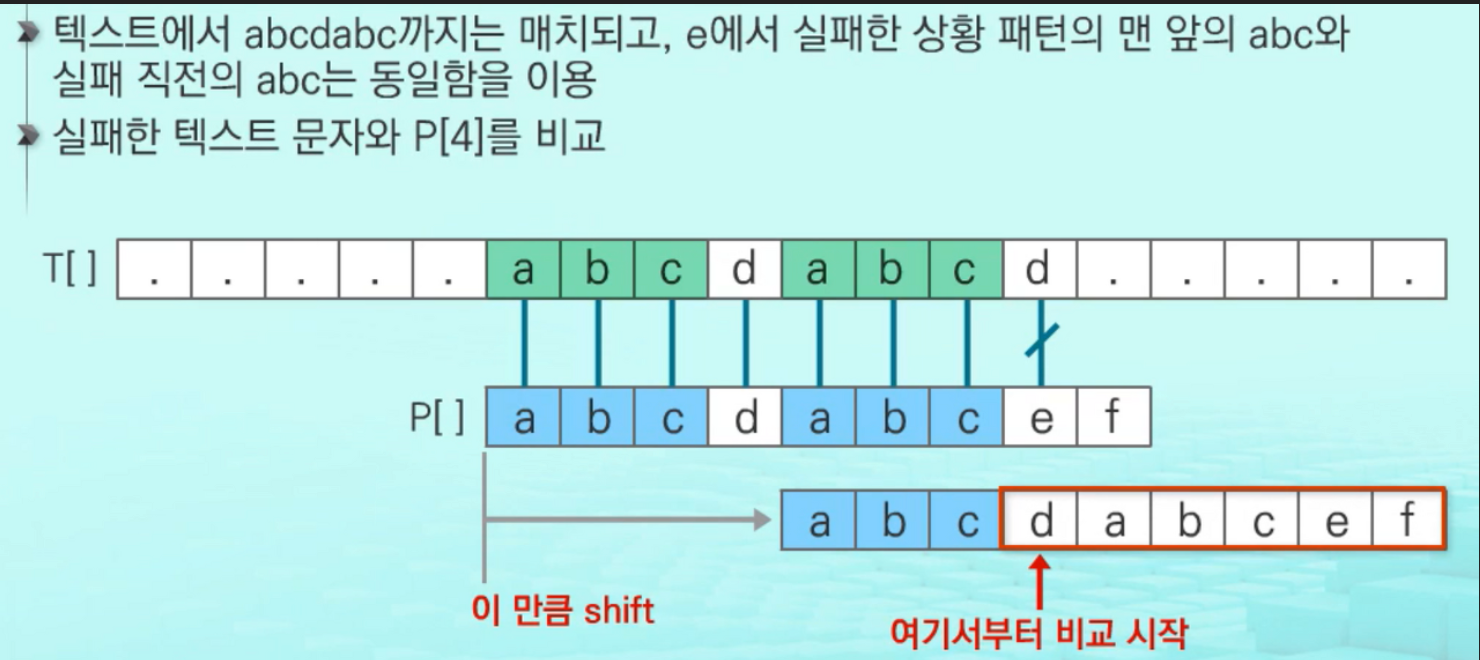
20.2.2.1 다음 시작 위치 찾기

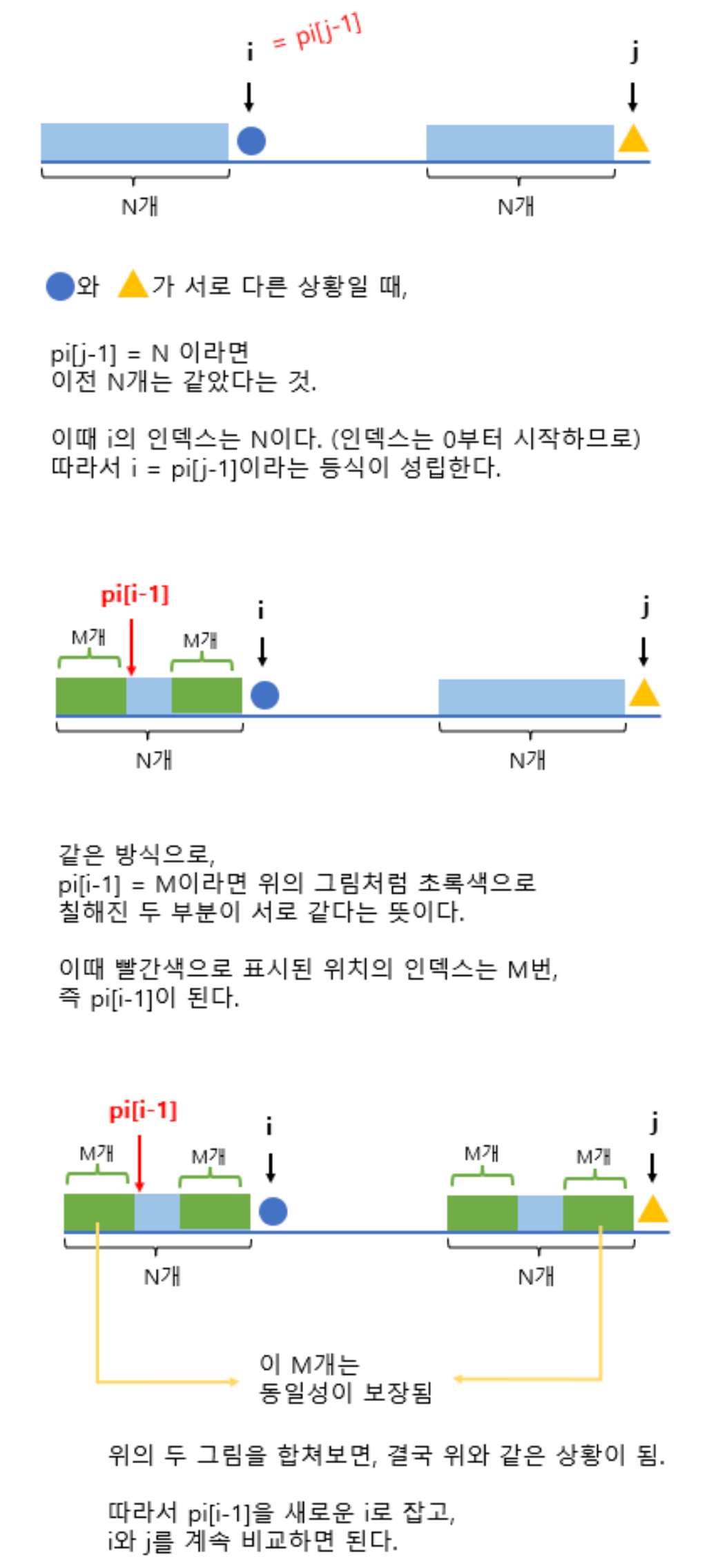
  • pi[i] = N[ : i+1]의 접두사도 되고 접미사도 되는 문자열의 최대 길이
  • pi[]는 N이 어디까지 일치했는지가 주어질 때 다음 시작 위치를 어디로 해야 할지를 말해 준다.
    • 부분 일치 테이블(partial match table) 이라고 부른다.

image-20240425164835715.png

image-20240425142752042.png

20.2.2.2 실제 문자열 검색의 구현

image-20240425154705618.png

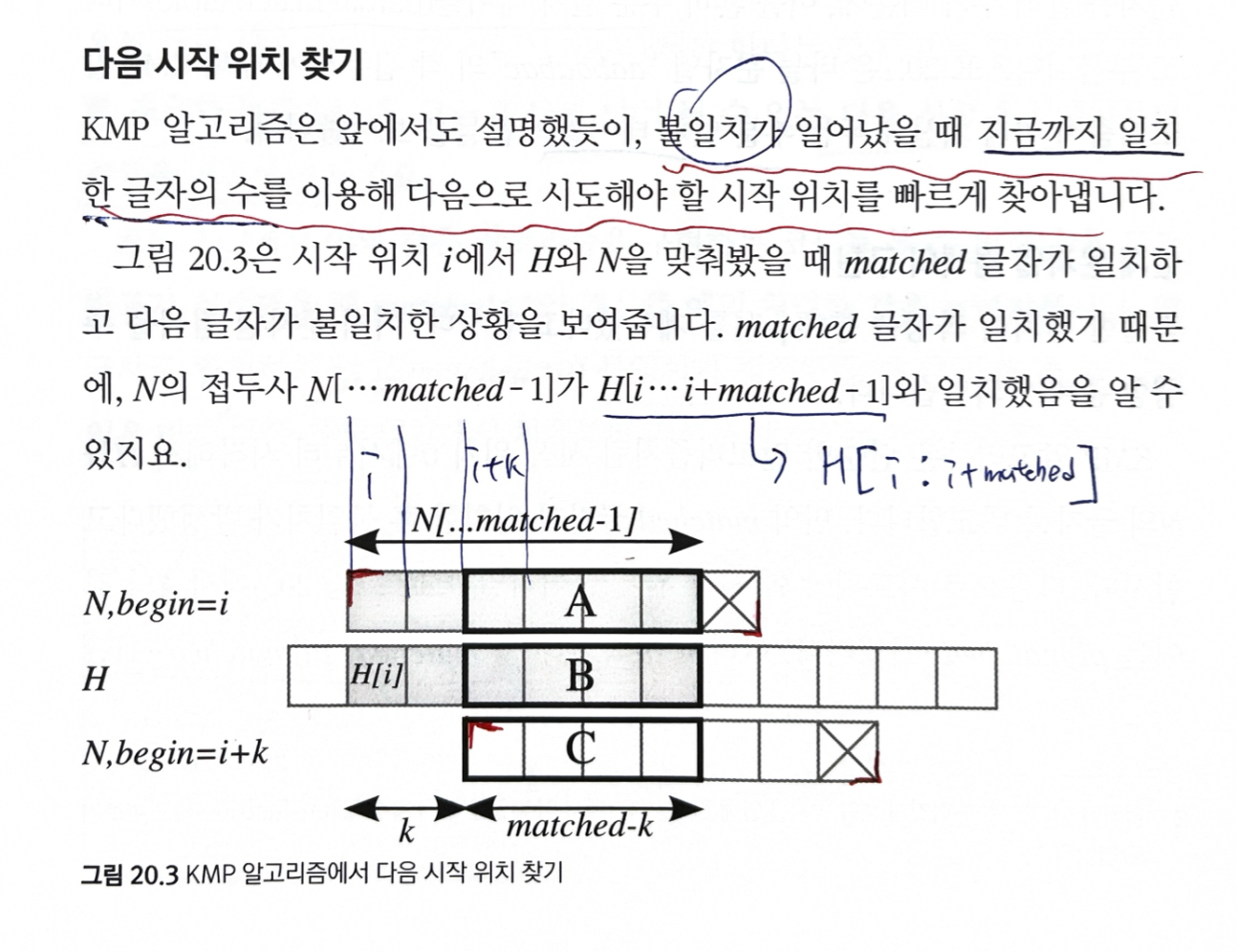
  • 적절한 전처리 과정을 통해 pi[]를 계산했다고 하자.
  • m(matched)가 일치한 후 불일치가 발생했다고 하자
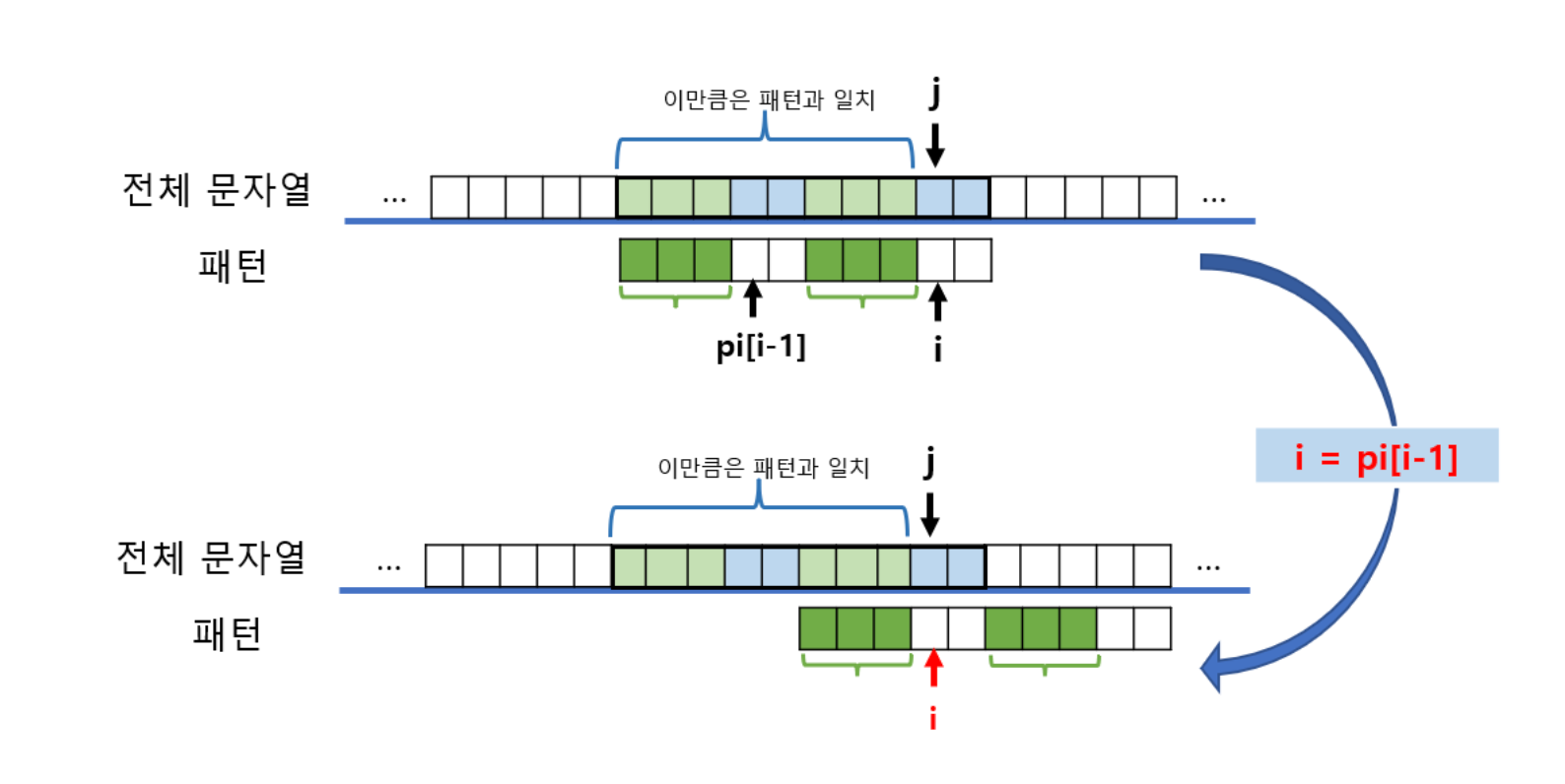
  • 다음 시작할 시작 위치:
    • m - pi[m-1] 만큼 증가
  • 새로운 위치에서 비교를 시작하더라도, N의 첫 pi[m-1] 글자는 대응되는 H의 글자와 일치
    • 따라서, m를 pi[m-1]으로 변경하고 비료를 계속하면 된다.
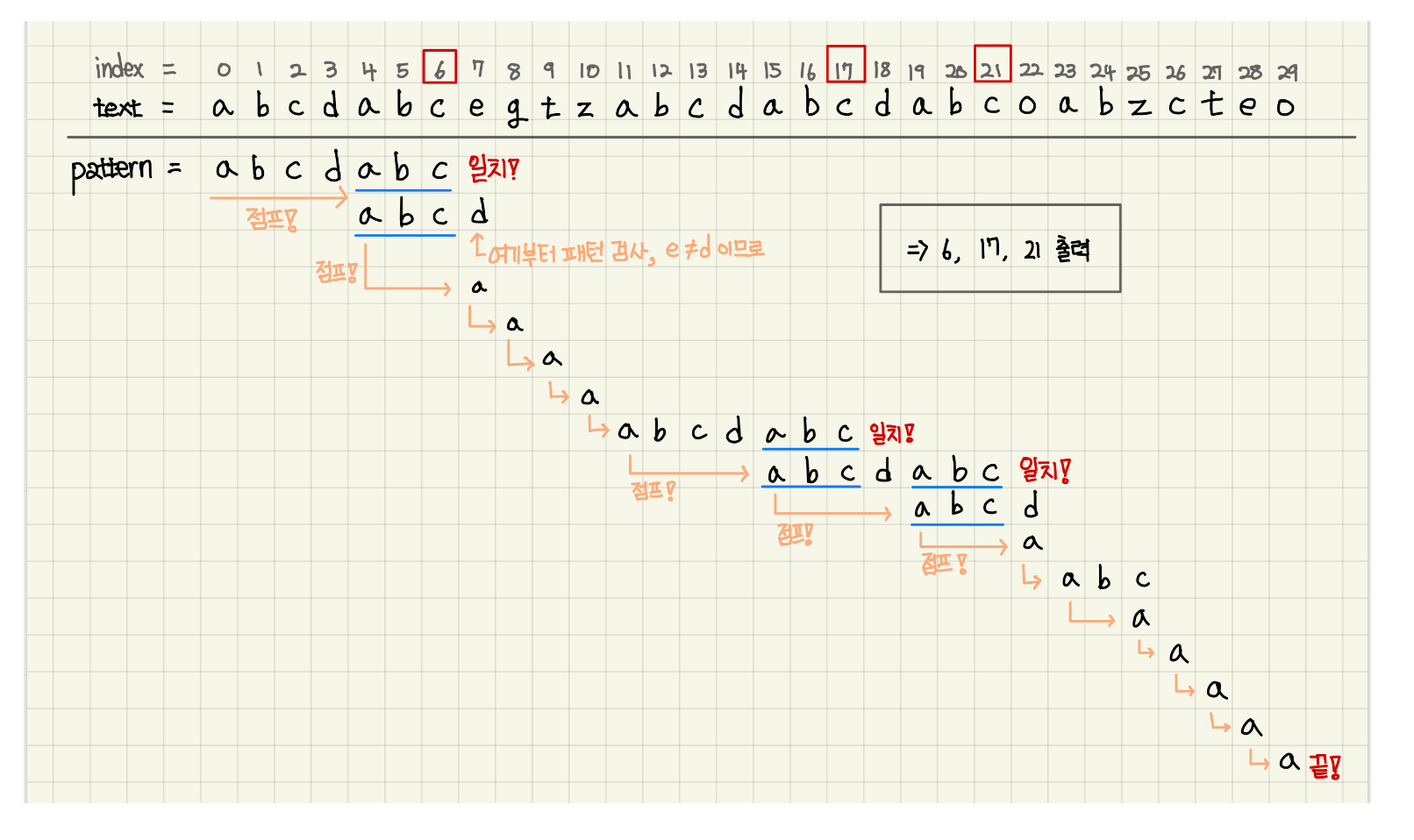
  • 불일치가 발생한 경우는 그렇다 치고, 답을 찾는 경우에는 어떻게 할까?
    • 현재 시작 위치를 답의 목록에 추가해야 한다는 것 빼고는 불일치가 발생한 경우와 똑같다.
    • 다음 시작 위치에서부터 검색을 계속하면 된다.

image-20240425142810947.png

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def kmp(Hstrs, Nstrs):
    lenH, lenN = len(Hstrs), len(Nstrs)
    pi, i = [0 for _ in range(lenN)], 0  # kmp_table
    for j in range(1, lenN):
        while i > 0 and Nstrs[i] != Nstrs[j]:
            i = pi[i - 1]

        if Nstrs[i] == Nstrs[j]:
            i += 1
            pi[j] = i

    result, i = [], 0  # kmp
    for j in range(lenH):
        while i > 0 and Nstrs[i] != Hstrs[j]:
            i = pi[i - 1]

        if Nstrs[i] == Hstrs[j]:
            i += 1
            if i == len(Nstrs):
                result.append(j - i + 1)
                i = pi[i - 1]

    return result

print(kmp('xabxxbaxbaxbaxbaxabxbaxbabx', 'abx'))  # [1, 17, 24]
print(kmp('abababab', 'abab'))  # [0, 2, 4]
# https://yiyj1030.tistory.com/495

20.2.2.3 시간 복잡도 분석

  • 문자 비교 성공은 짚더미(H)의 각 문자당 최대 한 번씩만 일어남: O(H)
  • if문의 비교는 최대 O(H)번 수행
  • 따라서 반복문의 전체 수행 횟수는 O(H) 이다.
  • 바늘(N)의 길이와 상관없이, 항상 짚더미(H)에만 비례

20.5 접미사 배열

image-20240425142840653.png

  • 문자열을 다룰 때 자주 쓰이는 자료 구조: 접미사 배열(suffix array)
  • 문자열 S의 모든 접미사를 사전순으로 정렬 해둔 것
  • 접미사들을 그대로 문자열 배열에 저장하면 문자열 길이의 제곱에 비례하는 메모리가 필요하기 때문에,
    • 보통 각 접미사의 시작 위치를 담는 정수 배열로 구현된다.
  • group[i] = S[i : ]가 속한 그룹의 번호

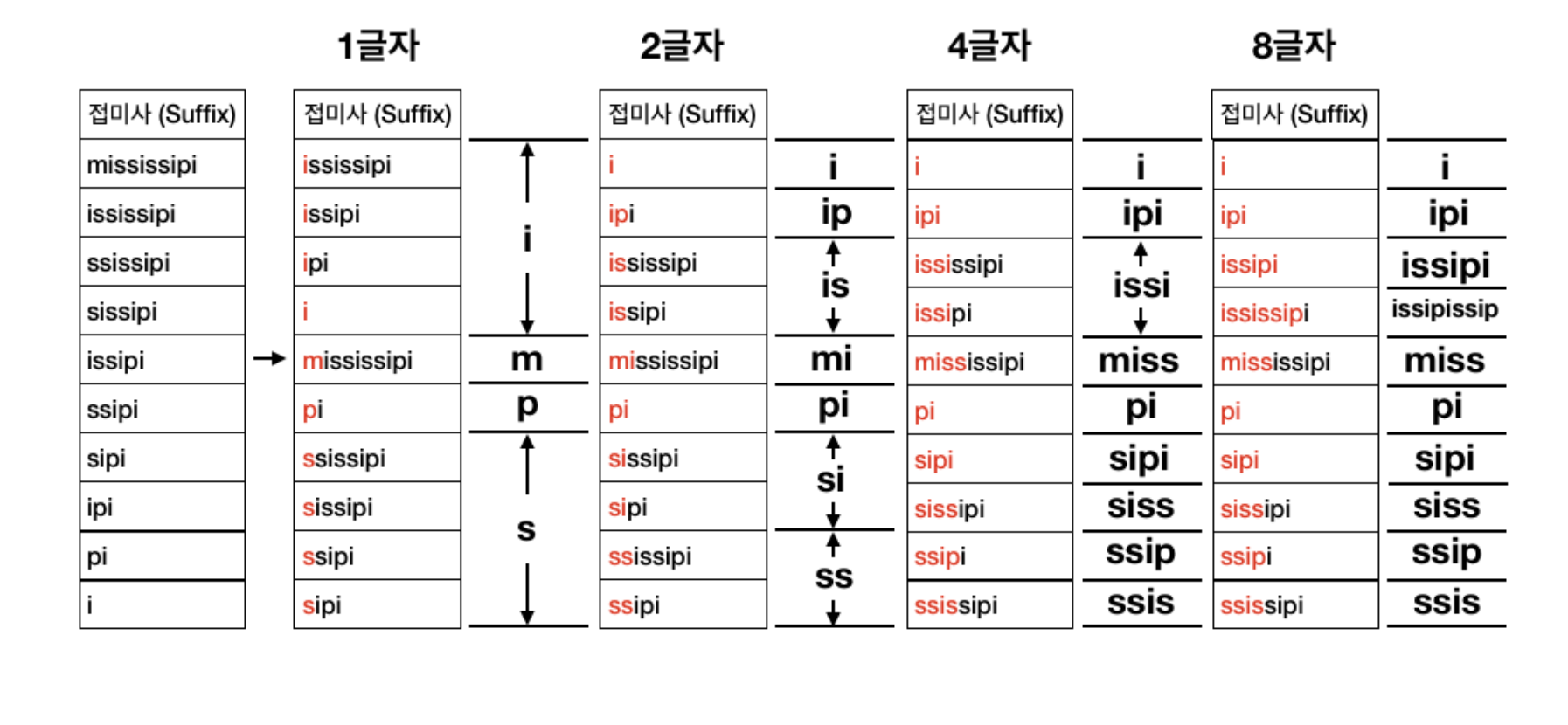
image-20240425142509931.png

20.5.1 접미사 배열을 만드는 맨버-마이어스(Manber & Myers)의 알고리즘

  • 문자열들이 모두 공통된 한 문자열의 접미사라는 점을 이용하여, 기수 정렬 (첫 1글자, 2글자, 4글자, …, 2^n 글자를 기준으로 정렬) 을 이용한 알고리즘이다.
  • 이렇게 log N 번 정렬을 하고 나면 원하는 접미사 배열을 얻을 수 있다.
  • 이렇게 정렬은 여러 번 하는데도 더 빠르게 동작하는 이유는 이전 정렬에서 얻은 정보를 이용해 두 문자열의 대소 비교를 O(1) 에 할 수 있기 때문이다.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def sortSuffix(text):  # 접미사 배열을 만드는 맨버-마이어스의 알고리즘
    n, suffix = len(text), []
    g = [0] * n
    g.append(-1)  # 현재 위치에서 t만큼 떨어진 위치가 없는 경우 rank를 -1로 설정
    t = 1

    for i in range(n):
        suffix.append(i)
        g[i] = ord(text[i]) - ord('a')

    while t < n:
        suffix.sort(key=lambda x: (g[x], g[min(x + t, n)]))
        ng = [0] * n
        ng.append(-1)
        for i in range(1, n):
            si, si_1 = suffix[i], suffix[i - 1]
            if g[si_1] != g[si] or g[min(si_1 + t, n)] != g[min(si + t, n)]:  # # rank가 다르면 서로 다른 rank 값을 갖게함
                ng[si] = ng[si_1] + 1
            else:  # rank가 같은 경우 서로 같은 rank
                ng[si] = ng[si_1]

        g = ng
        if ng[n - 1] == n - 1: break
        t *= 2

    return suffix

# https://codable.tistory.com/14
  • 전체 시간 복잡도: O(N lg^2N)
    • 기존, O(N^2 lgN)에 비해 큰 발전

Reference