22. 이진 검색 트리
22.1 도입
- 검색 트리(search tree) 는 연결 리스트, 큐 처럼 자료들을 담는 컨테이너지만, 자료들을 일정한 순서에 따라 정렬한 상태로 저장합니다.
- 주어진 순서에 따라 자료들을 저장하는 리스트와 큐와는 다른 속성
- 이러한 특성을 이용해, 추가, 삭제, 존재 여부 확인 등 다양한 연산을 빠르게 수행
- 검색 트리에서 가장 흔하게 사용하는 것이 이진 검색 트리(binary search tree)와 그 변종들 이다.
22.2 이진 검색 트리의 정의와 조작
22.2.1 정의
이진 트리(binary tree): 각 노드가 왼쪽, 오른쪽 최대 두 개의 자식 노드만을 가질 수 있는 트리
- 자식 노드들의 배열 대신 두개의 포인터 left, right를 담는 객체로 구현
이진 검색 트리는 이진 탐색에서 아이디어를 가져와서 만든 트리이다.
우리가 N개의 원소 중에서 원하는 값을 찾는데, 매번 후보의 수를 절반씩 줄여갈 수 있다면 O(logN) 시간에 그 값을 찾을 수 있다.
이진 검색 트리의 각 노드는 하나의 원소(value)를 가지고 있다.
왼쪽 서브 트리에는 해당 노드의 원소보다 작은 원소를 가진 노드들
오른쪽 서브 트리에는 보다 큰 원소를 가진 노드들이 들어간다.
22.2.2 순회
- 이진 검색 트리는 중위 순회를 하면 크기 순서로 정렬된 원소의 목록을 얻을 수 있다.
- 집합에 포함된 최대 원소나 최소 원소를 쉽게 얻을 수 있다는 의미
왼쪽 연결로 쭉 내려갔을 때 만나는 노드:최소 원소,가장 일찍 출력되는 노드오른쪽 연결로 쭉 내려갔을 때 만나는 노드:최대 원소,가장 마지막에 출력되는 노드
22.2.3 자료의 검색
- 한 번 원소를 비교하는 것 만으로도 찾아야 할 전체 대상의 절반을 줄일 수 있다.
- 실질적으로 이진 탐색과 비슷한 속도를 자료를 찾을 수 있다.
22.2.4 조작 (추가, 삭제)
추가, 삽입
- 선형적인 구조의 제약이 없기 때문에, 새 원소가 들어갈 위치를 찾고, 거기에 노드를 추가하기만 하면 간단히 가능
- 추가, 삽입은 새 리프(잎) 노드가 생길 뿐이므로, 트리 전체의 구조에는 영향이 없음
삭제
삭제는 트리 어디서든 일어날 수 있어, 트리 전체의 구조에 영향을 주므로 여럽다.
간단한 방법:
'합치기'연산을 구현- 노드 t를 지울 거라면, t의 두 서브트리를 합친 새로운 트리를 만든 뒤, 이 트리를 t를 루트로 하는 서브트리와 바꿔치기
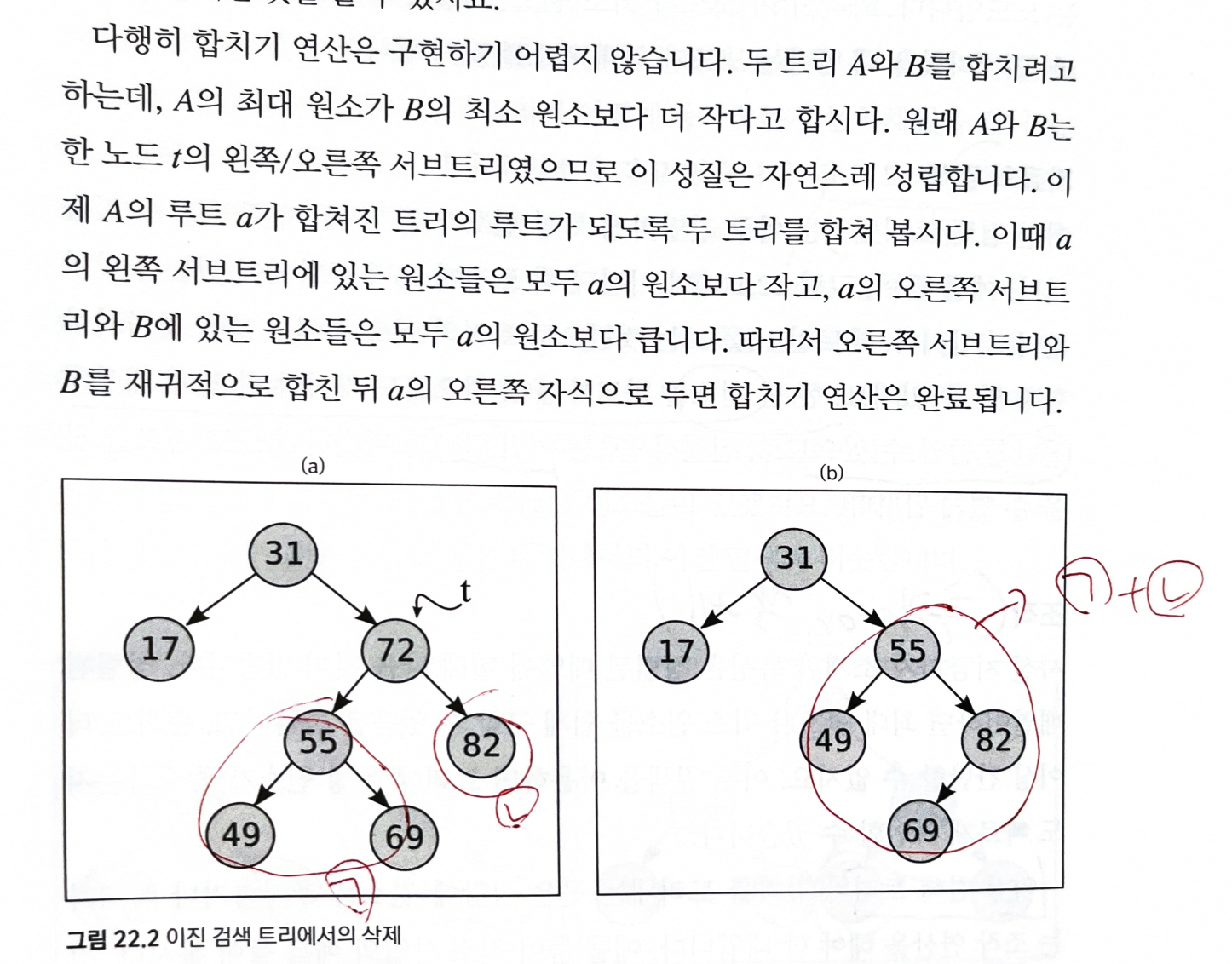
22.2.5 X보다 작은 원소의 수 찾기 / k번째 원소 찾기
- 표준 라이브러리에서 지원하는 언어는 거의 없기 때문에, 이 연산을 사용하려면, 직접 이진 검색 트리를 구현할 수 밖에 없다.
- 실제 구현은
트립의 구현을 다루는 22.6절 을 참고
- 실제 구현은
22.3 시간 복잡도 분석과 균형 잡힙 이진 검색 트리
- 이진 검색 트리에 대한 모든 연산은 모두 루트에서 부터 한 단계씩 트리를 내려가며 재귀 호출을 통해 수행된다.
- 최대 재귀 호출의 횟수는 트리의 높이 h와 같다.
- 따라서 모든 연산의 시간 복잡도가 트리의 높이
O(h)라 할 수 있다.
- 이진 검색 트리의 높이는 자료들이 어떤 순서로 추가, 삭제되느냐에 따라 다르다.
- 극단적인 경우 한쪽으로만 노드가 있어서 기울어진(skewed) 트리가 될 수도 있다. (연결리스트와 다를 게 없다)
- 우리가 원하는 이상적인 경우는 가로로 넓게 퍼지고 ‘평평한’ 트리 이다.
- 트리의 높이가 1 높아질 때마다 트리에 들어갈 수 있는 원속의 수가 대략 두 배 늘어간다
- 트리의 최소 높이(h)는 O(logN)이다
균형 잡힌 이진 검색 트리 (balanced binary search tree)- 이진 검색 트리의 변종, 기울어짐 방지
- 트리의 구조에 추가적인 제약을 둠, 이 제약을 만족되도록 노드들을 옮김
- 트리의 높이가 항상 O(logN)이 되도록 유지
- 대표적인 예시: 레드-블랙(red-black) 트리, AVL 트리
- 이진 검색 트리의 구현도 내부적으로는 레드-블랙(red-black) 트리을 사용한다.
22.6 균형 잡힙 이진 검색 트리 직접 구현하기: 트립
- 대부분의 균형 잡힌 이진 검색 트리들(AVL 트리, 레드-블랙 트리) 은 구현이 매우 까다롭다.
- 코드가 길고, 한정된 시간 안에 코드를 작성해야하는 프로그래밍 대회에서 사용하기 부적합
- 따라서, 구현이 간단한 이진 검색 트리를 사용:
트립(treap, tree+heap)
22.6.1 트립의 정의
- 트립은 입력이 특정 순서로 주어질 때 그 성능이 떨어진다는 이진 검색 트리의 단점을 해결하기 위해 고안된 랜덤화된 이진 검색 트리이다.
- 트립은 원소들의 추가 순서에 따라 결정되지 않고, 난수에 의해 임의로 결정된다.
- 어느 순서대로 추가, 삭제 되더라도, 트리 높이의 기대치는 항상 일정하다.
- 이 속성을 위해서, 트립은 새 노드가 추가될 때 마다 해당 노드에 우선순위(priority) 를 부여한다.
- 우선순위 값은 난수 이다.
- 트립을 이해하는 또 다른 방법: 노드들을 우선순위가 높은 것부터 순서대로 추가한 이진 검색 트리
트립의 조건 2가지
이진 검색 트리의 조건
왼쪽 서브 트리에는 해당 노드의 원소보다 작은 원소를 가진 노드들
오른쪽 서브 트리에는 보다 큰 원소를 가진 노드들이 들어간다.
힙의 조건: 모든 노드의 우선순위는 각자의 자식 노드보다 크거나 같다.
Reference
- 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 (구종만, 인사이트)
- https://www.algospot.com/