06장. 트리 정리

  • ch23. 우선운위 큐와 힙

23. 우선운위 큐와 힙

23.1 도입

  • 우선순위 큐 에서는 가장 먼저 입력된 자료가 가장 먼저 꺼내지는 것이 아니라, 우선순위가 가장 높은 자료가 가장 먼저 꺼내진다.
  • 균형 잡힌 이진 검색 트리를 사용해서 우선순위 큐를 구현할 수 있다.
    • 하지만 이는 소 잡는 칼로 닭을 잡는 것과 같다.
    • 휠씬 단순한 구조로도 구현할 수 있다.
  • 힙(heap) 이라는 이진 트리 자료구조로 우선순위 큐를 구현 할 수 있다.
    • 여기서는 최대 힙이라 가정
  • 힙은 대부분의 프로그래밍 언어의 표준 라이브러리에 구현되어 있다.

23.2 힙의 정의와 구현

  • 힙의 대소 관계 규칙: 부모 노드가 가진 원소는 항상 자식 노드가 가진 원소 이상이다. (최대 힙의 경우)

    • 가장 중요하고 기본적인 규칙
    • 이진 검색 트리와 달리 부모 자식 관계에만 적용
    • 왼쪽, 오른쪽 자식이 갖는 원소의 크기는 제한하지 않는다.

  • 힙의 모양 규칙: 이진 검색 트리에서도 문제가 되었던, 트리가 기울어지는 일을 막음

    1. 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다.

    2. 마지막 레벨에 노드가 있을 때는 항상 가장 왼쪽 부터 순서대로 채워져 있어야 한다.

  • 힙의 높이: O(logN)

23.2.1 배열을 이용한 힙의 구현

  • 힙이 요구하는 엄격한 모양 규칙은 구현할 때는 장점이다.

    • 트리에 포함된 노드의 개수만 알면 트리 전체의 구조를 알 수 있기 때문이다.

    • 동적 배열은 힙에 들어 있는 원소들을 맨 윗 레벨 부터, 왼쪽에서 오른쪽 순서대로 저장한다.

  • A[i] 에 대응되는 노드의 왼쪽 자손은 A[2*i+1] 에 대응

  • A[i] 에 대응되는 노드의 오른쪽 자손은 A[2*i+2] 에 대응

  • A[i] 에 대응되는 노드의 부모는 A[(i-1) / 2 ]에 대응 (나눗셈 결과는 내림)

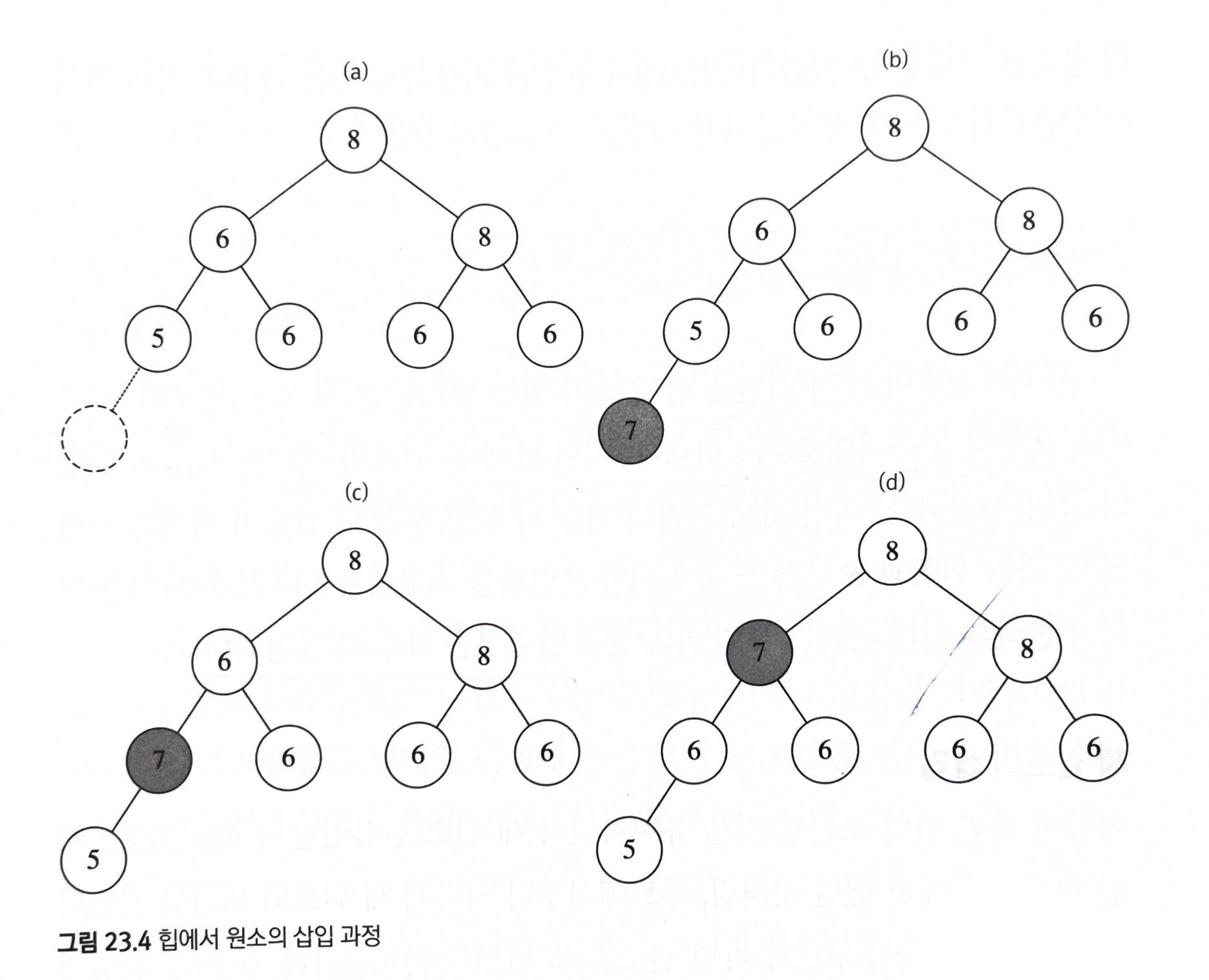
23.2.2 새 원소의 삽입(push)

  • 힙에서 새 원소를 삽입(push) 할때는 간단한 방법은 대소 관계 규칙 대신 모양 규칙을 먼저 만족시키는 것이다.
    • 모양 규칙에 의해 새 노드는 항상 heap배열 에 맨 끝에 추가된다.
    • 마직막에 추가한 새 원소를 자신의 부모와 비교
    • 비교 후, 작다면 두 원소의 위치를 바꾼다.
    • 새 원소가 더 크거나 같은 원소를 가진 부모를 만나거나, 루트에 도달할 때까지 이를 반복한다.
    • push(삽입) 의 시간복잡도: 트리의 높이인 O(logN)

image-20240408201050665.png

23.2.3 최대 원소 꺼내기(pop)

  • 배열을 이용한, 최대 힙에서 최대 원소를 찾는 것은 첫 원소를 확인하면 된다. 매우 간단
  • 문제는, 최대 원소를 힙에서 꺼내는 것(삭제, pop) 이다.
  • 삭제에서도, 삽입과 같이 간단한 방법은 대소 관계 규칙 대신 모양 규칙을 먼저 만족시키는 것이다.
    • 힙의 마지막에 있는 리프 노드를 삭제
    • 마지막 노드에 있던 원소는 루트로 덮어 씌움
    • 두 자식 노드가 가진 원소 중 더 큰 원소를 선택해 루트가 갖고 있는 원소와 맞바꿈.
    • 이 작업을 트리의 바닥에 도달하거나, 두 자손이 모두 자기 자신 이하의 우너소를 갖고 있을 때 까지 반복
    • pop(삭제) 의 시간복잡도: 트리의 높이인 O(logN)

image-20240408201202012.png

23.2.4 다른 연산들

  • 힙을 만드는 연산(heapify)

    • N개의 원소를 텅 빈 힙에 순서대로 삽입해야 할 때 쓸 수 있다.
    • 원소들을 길이가 N인 배열에 저장한 뒤, heapify 연산을 수행하면, O(N)만에 힙으로 만들어 준다.
    • push( O(logN) ) 연산을 N번 호출하는, O(NlogN)에 비해 빠르지만,
    • 어차피, N개의 원소를 다시 꺼내는 데만도 O(NlogN) 시간이 걸리고, 이것을 프로그램의 수행 시간을 지배해 버리기 때문에 큰 의미는 없다.

  • 힙 정렬(Heapsort)

    • 힙에서 원소들을 꺼낼 때, 항상 정렬된 순서대로 반환된다는 점을 이용

    • 배열을 힙으로 만든 뒤, 모든 원소들을 꺼내서 반환 순서대로 배열하면 정렬 결과가 된다.

    • 이때 힙에서 원소를 하나 꺼내면, 힙을 담은 배열의 맨 뒤쪽이 한 칸 비게 되므로,

      • 최대 원소를 여기에 옮기면 추가 메모리를 사용하지 않고 정렬 가능

    • 최악의 경우에도 O(NlogN) 의 시간복잡도, 병합 정렬과 달리 추가적인 메모리 요구하지 않음

Reference