25. 상호 배타적 집합

25.1 도입

  • 유니온-파인드(Union-Find) 라는 트리 자료구조로 상호 배타적 집합(disjoint set)을 표현할 수 있다.

25.1.1 상호 배타적 집합

  • 공통 원소가 없는, 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 정보를 저장, 조작하는 자료구조가 유니온-파인드 자료구조 이다.
  • 연산
    • 초기화(init): n개의 원소가 각각의 집합에 포함되어 있도록 초기화
    • 합치기(union): 두 원소 a,b 가 주어질 때 이들이 속한 두 집합을 하나로 합침
    • 찾기(find): 어떤 원소 a가 주어질 때 이 원소가 속한 집합을 반환

25.1.2 배열로 상호 배타적 집합 표현

  • 상호 배타적 집합을 표현하는 가장 간단한 방법: 1차원 배열
    • belongsTo[i] = i번 원소가 속하는 집합의 원소
    • 문제 상황: 찾기 연산은 O(1)이지만, 합치기 연산은 O(N) 이다.
    • 넣음찾기 연산이 조금 오래 걸리더라도, 합치기 연산을 빠르게 할 수 없을까?

25.1.3 트리를 이용한 상호 배타적 집합 표현

  • 한 집합에 속하는 원소들을 하나의 트리로 묶어 준다.

  • 따라서, 상호 배타적 집합 자료구조는 트리들의 집합으로 표현된다.

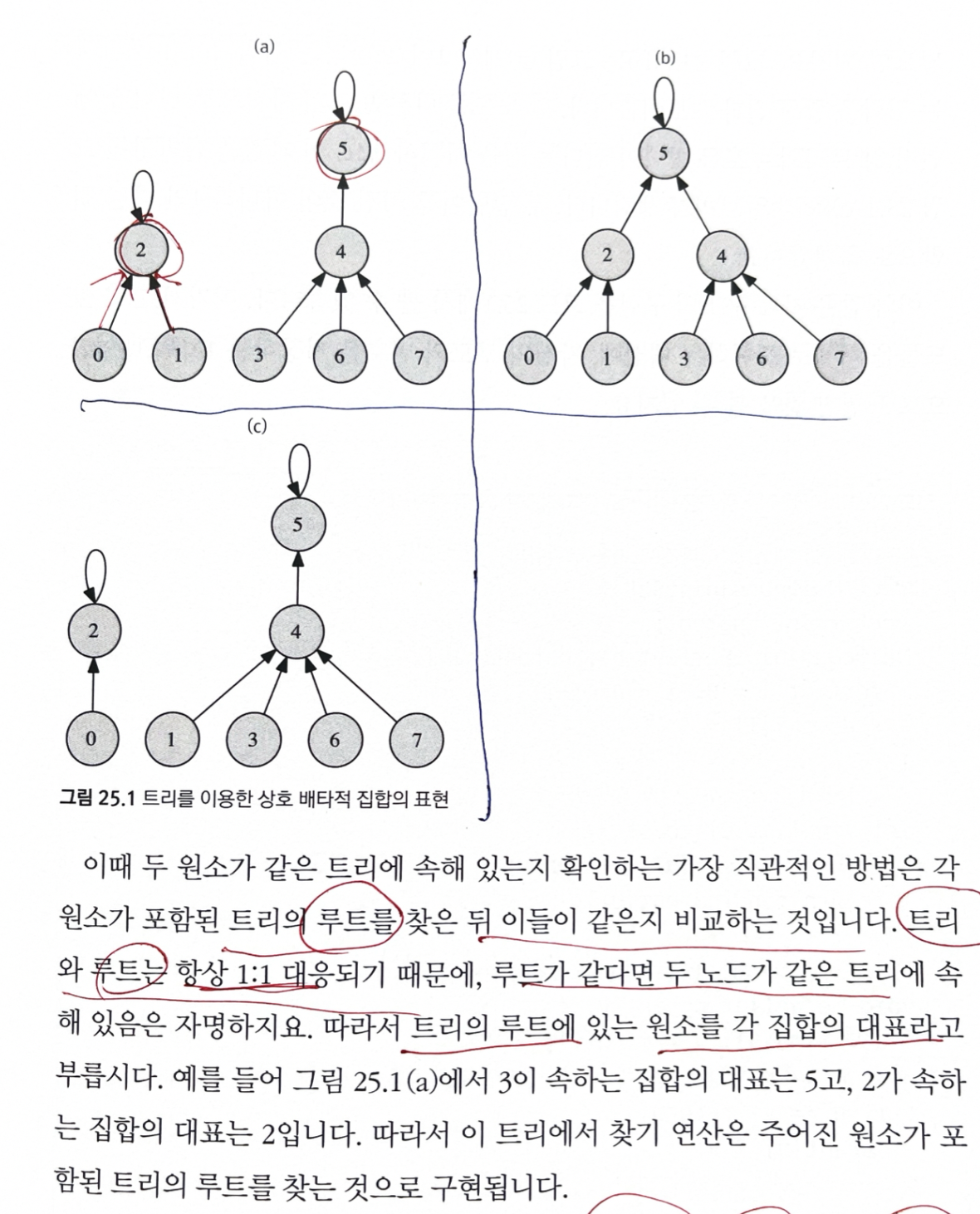
  • 이때, 두 원소가 같은 트리에 속해 있는 지 확인하는 직관적인 방법은 원소가 포함된 트리의 루트를 찾은 뒤 이들이 같은지 비교하는 것

  • 트리와 루트는 항상 1:1 대응되기 때문에, 루트가 같다면 두 노드가 같은 트리에 속해 있다.

  • 따라서, 트리의 루트에 있는 원소(루트 값)를 각 집합의 대표라고 부르자.

  • 이런 연산을 구현 하기 위해서는, 모든 자식 노드가 부모에 대한 포인터를 가지고 있어야 한다.

    • 부모는 자식으로 내려갈 일이 없기 때문에 부모는 자식에 대한 포인터를 가질 필요가 없다.
    • 루트는 부모가 없으므로, 대게 자기 자신을 가리키도록 구현

  • 간단해진 합치기 연산: 각 트리의 루트를 찾은 뒤, 하나를 다른 한쪽의 자손으로 넣으면 된다.

    • 합치기, 찾기 연산의 시간복잡도 모두: 트리의 높이에 비례

image-20240409142928425.png

25.1.4 상호 배타적 집합의 최적화

  • 문제 상황 1: 트리를 사용하면, 연산의 순서에 따라 트리가 한쪽으로 기울어진다.

    • 기울어지면, 찾기, 합치기 연산모두 O(N)으로 되어버림
    • 배열로 구현한것 보다 오히려 더 효율이 나빠져 버림

  • 해결, 최적화 방법: 항상 높이가 더 낮은 트리를 더 높은 트리 밑에 집어넣음으로써 트리의 높이가 높아지는 상황을 방지

    • => 랭크에 의한 합치기 (union-by-rank) 최적화

    • 합치기, 찾기 연산 시간복잡도 모두 O(logN)

    • 기존 O(N)에서 계선 됨

  • 문제 상황 2: 찾기 연산이 중복된 연산을 여러 번 하고 있다.

  • 해결, 최적화 방법: 경로 압축(path compression) 최적화

    • find(u) 를 통해 u가 속하는 트리의 루트를 찾았을 때, parent[u] 를 찾아낸 루트로 아예 바꿔 버리면
    • 다음 번에 find(u) 를 호출할 때, 경로를 따라 올라 갈 것 없이 바로 루트를 찾을 수 있게 된다.

  • 재귀적으로 find() 를 구현

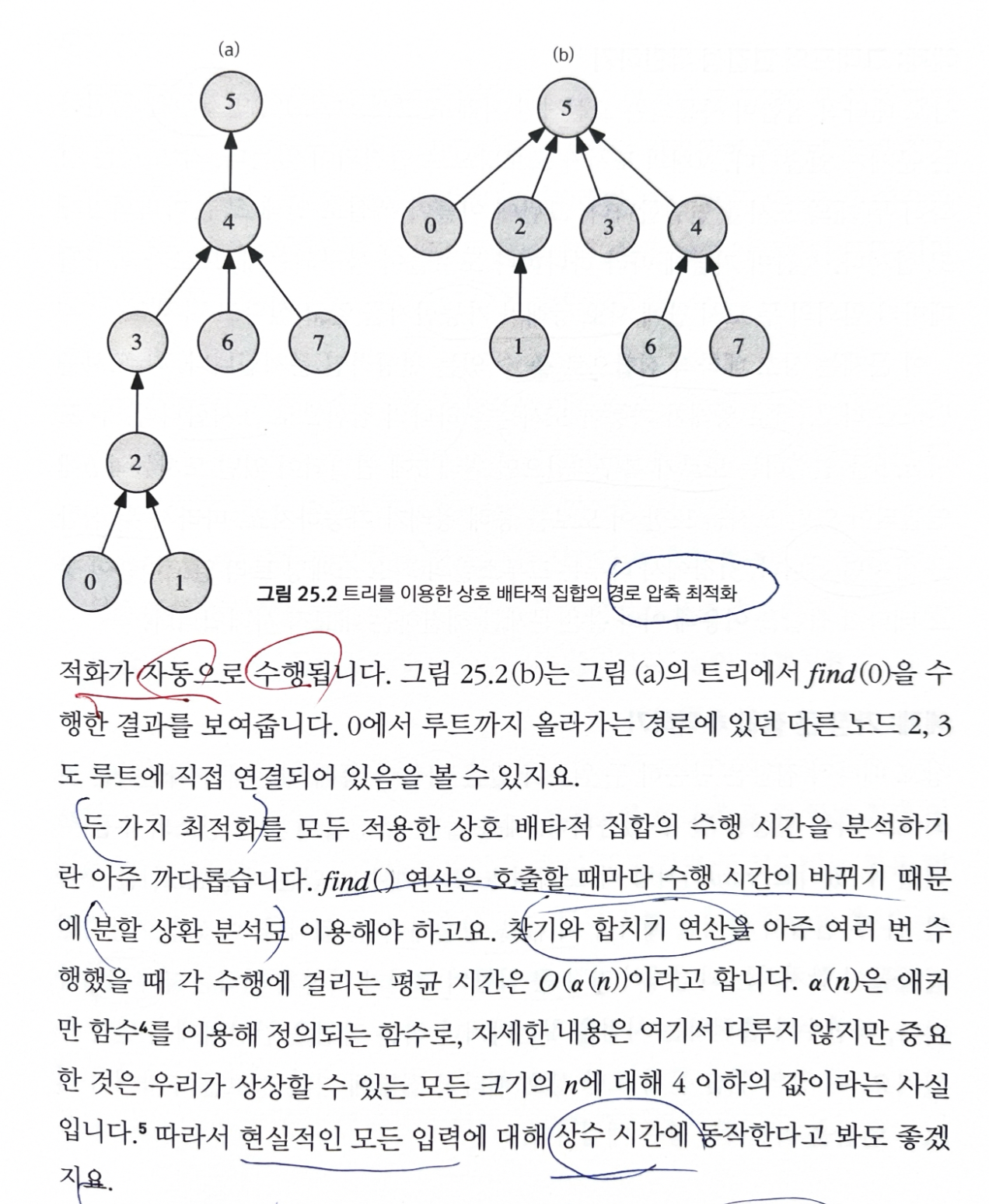
    • 재귀적인 구현 덕분에 find(u)를 호출하면 u에서 루트까지 올라가는 경로 상에 있는 모든 노드들에도 경로 압축 최적화 가 자동으로 수행

  • 시간 복잡도

    • 수행 시간 분석하기 아주 까다로움, 분할 상환 분석 등 이용해야 함.
    • 현실적인 입력에 대해, 합치기, 찾기 연산 모두 상수 시간에 동작한다고 봐도 무방

image-20240409142837742.png

25.1.5 상호 배타적 집합이 사용되는 경우

  • 그래프의 연결성 확인

    • 그래프의 노드들이 서로 왕래가 가능한지 알고 싶을 때

    • 서로 왕래가 가능한 도시들을 하나의 집합으로 표현

  • 가장 큰 집합 추적하기

    • 각 집합에 속한 원소의 수를 추적
    • size[] 배열을 추가 한 뒤, 두 집합이 합쳐질 때 마다 이 값을 갱신
    • 집합들이 합쳐지는 과정에서, 가장 큰 집합의 크기가 어떻게 변하는지 추적 가능

25.2 유니온-파인드 Python 코드 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

global parent

def init():
    parent = [0 for _ in range(N + 1)]
    for i in range(0, N + 1):
        parent[i] = i

def find(a):
    if a == parent[a]:
        return a
    else:
        parent[a] = find(parent[a])
        return parent[a]

def union(a, b):  # union 연산, 대표 노드끼리 합치기
    a = find(a)
    b = find(b)
    if a != b:
        parent[b] = a

        
for i in range(M): # solution
    q, a, b = map(int, input().split())
    if q == 0:
        union(a, b)
    elif q == 1:
        if find(a) == find(b):
            print("YES")
        else:
            print("NO")

Reference