26. 트라이

26.1 도입

image-20240425150132131.png

  • 문자열 변수를 비교하는 데는 최악의 경우 문자열의 길이에 비례하는 시간이 걸릴 수 있다.

  • 탐색 자료 구조들도 시간이 너무 오래 걸릴 수 있다.

  • 이와 같은 문제를 해결하기 위해 고안된 문자열 특화 자료 구조: 트라이(Trie)

  • 집합 내에서 원하는 원소를 찾는 작업을 O(M), M은 문자열의 최대 길이

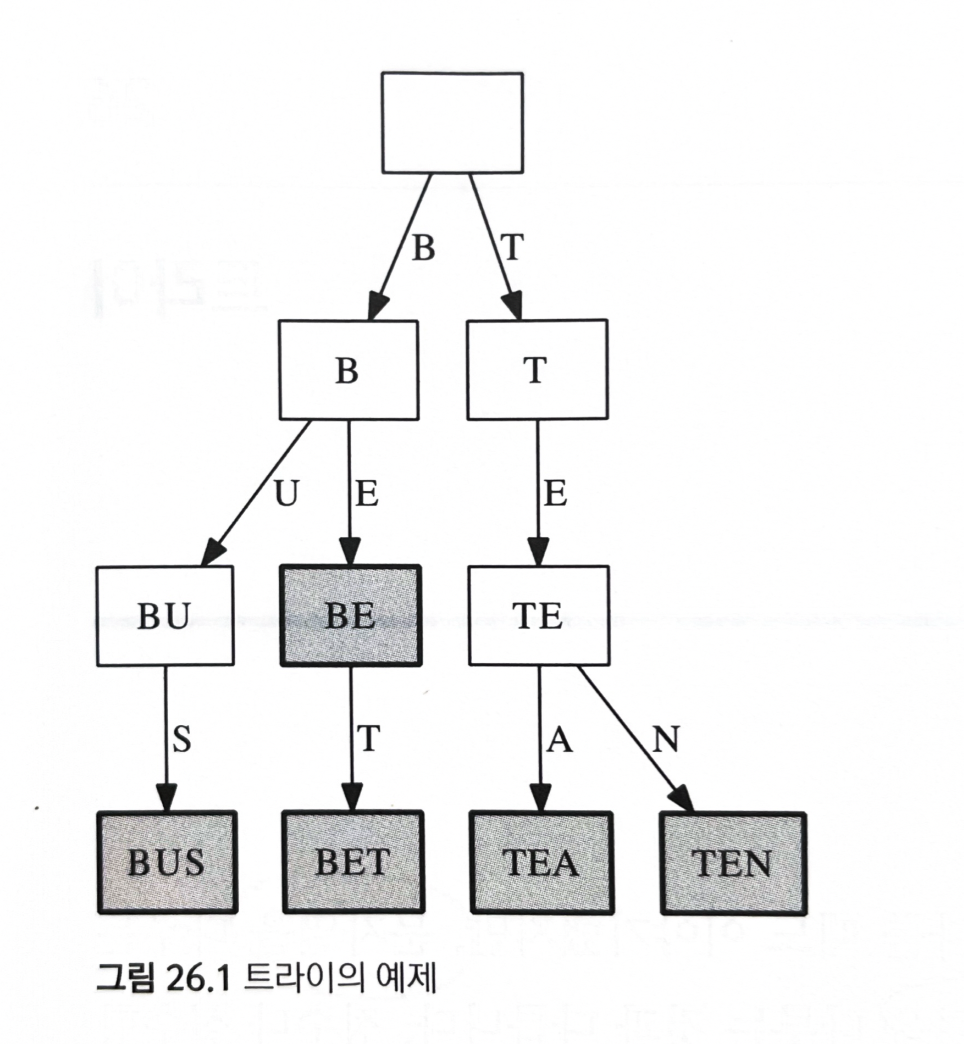
  • 트라이는 접두사들에 대응되는 노드들이 서로 연결된 트리

    • 한 접두사의 맨 뒤에 글자를 덧붙여 다른 접수사를 얻을 수 있을 때, 두 노드는 부모-자식 관계로 연결

  • 트라이의 루트는 항상 길이 0인 문자열에 대응

  • 노드의 깊이가 깊어질 때마다 대응되는 문자열의 길이가 1씩 늘어난다.

  • 루트에서 한 노드까지 내려가는 경로에서 만나는 글자들을 모으면 해당 노드에 대응되는 접두사를 얻을 수 있다.

  • 트라이는 포함하는 문자열들의 모든 접두사에 대응되는 노드들을 가지고 있기 때문에,

    • 전체 문자열이 아닌 문자열의 첫 일부만을 가지고도 이 문자열로 시작하는 키가 있는지 쉽게 확인 가능
    • 자동 완성을 구현할 때 유용

  • 자손 노드들을 가리키는 포인터 목록을 동적 배열로 구현하는 것이 아니라, 고정 길이 배열로 구현

    • 알파벳 대문자로만 구성된 문자열을 저장하는 트라이의 각 노드는 각 노드가 26개짜리 포인터 배열을 가지고 있다.

    • 다음 노드를 찾는 과정에서 어떤 탐색도 필요하지 않다. (고정됨)

    • 대신, 트라이의 최대 문제는 필요로 하는 공간이 너무 크다는 것

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

class Node(object):
    def __init__(self, isEnd):
        self.isEnd = isEnd
        self.childNode = {}

class Trie(object):
    def __init__(self):
        self.parent = Node(None)

    def insert(self, string):  # 문자 삽입

        nowNode = self.parent
        temp_length = 0
        for char in string:
            if char not in nowNode.childNode:  # 자식 Node들 미생성된 문자열이면 새로 생성

                nowNode.childNode[char] = Node(char)
            nowNode = nowNode.childNode[char]  # 자식 노드로 이동
            temp_length += 1
            if temp_length == len(string):
                nowNode.isEnd = True

    def search(self, string):  # 문자열이 존재하는지 탐색
        nowNode = self.parent
        temp_length = 0
        for char in string:
            if char in nowNode.childNode:
                nowNode = nowNode.childNode[char]
                temp_length += 1
                if temp_length == len(string) and nowNode.isEnd == True:
                    return True
                else:
                    return False
            else:
                return False

N, M = map(int, input().split())
myTrie = Trie()
for _ in range(N):
    word = input().strip()
    myTrie.insert(word)

result = 0
for _ in range(M):
    word = input().strip()
    if myTrie.search(word):
        result += 1

print(result)

26.1.1 접미사 트리

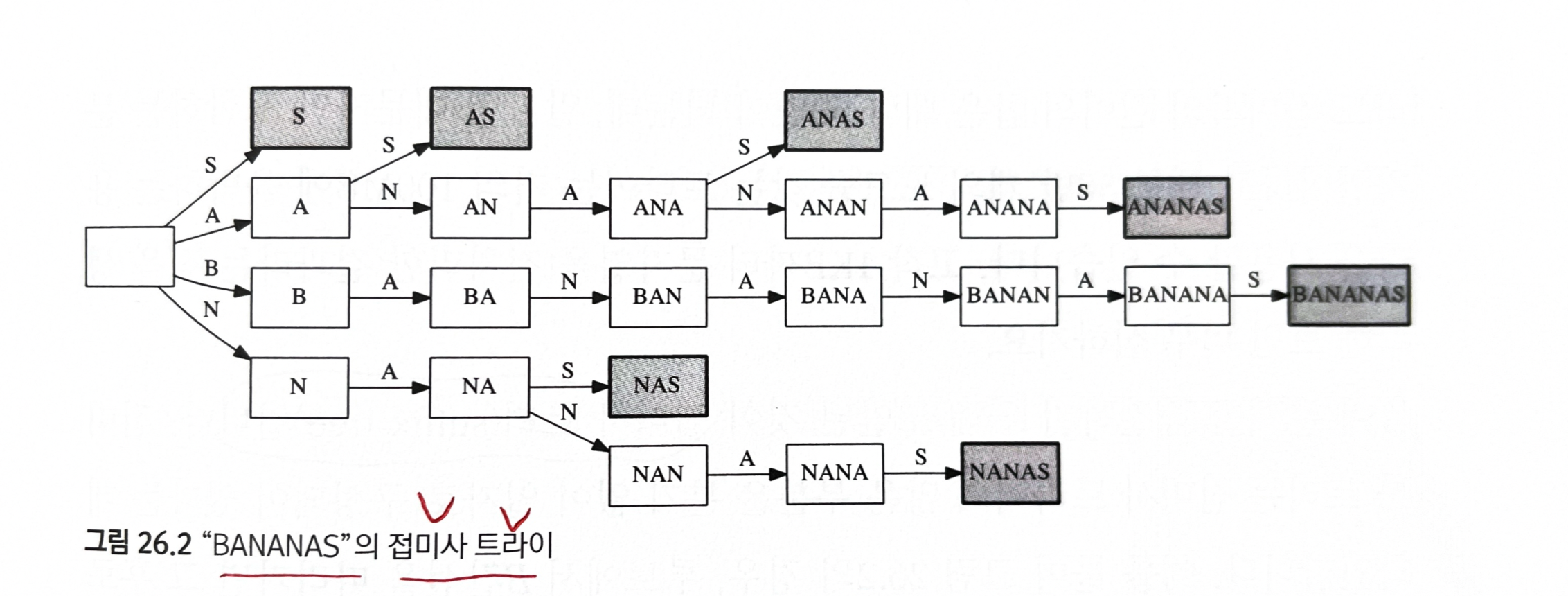
image-20240425150156891.png

  • 문자열의 모든 부분 문자열은 결국 어떤 접미사의 접두사이다.
  • 트라이는 저장된 문자열의 모든 접두사들을 저장한다.
    • 접미사 트라이는 이 문자열의 모든 부분 문자열에 대응되는 노드를 가지고 있다.
    • 따라서, 접미사 트라이에서의 검색을 이용하면 어떤 부분 문자열도 빠르게 찾을 수 있다.
    • 접미사 ‘트라이’ 는 메모리를 너무 많이 차지 한다.

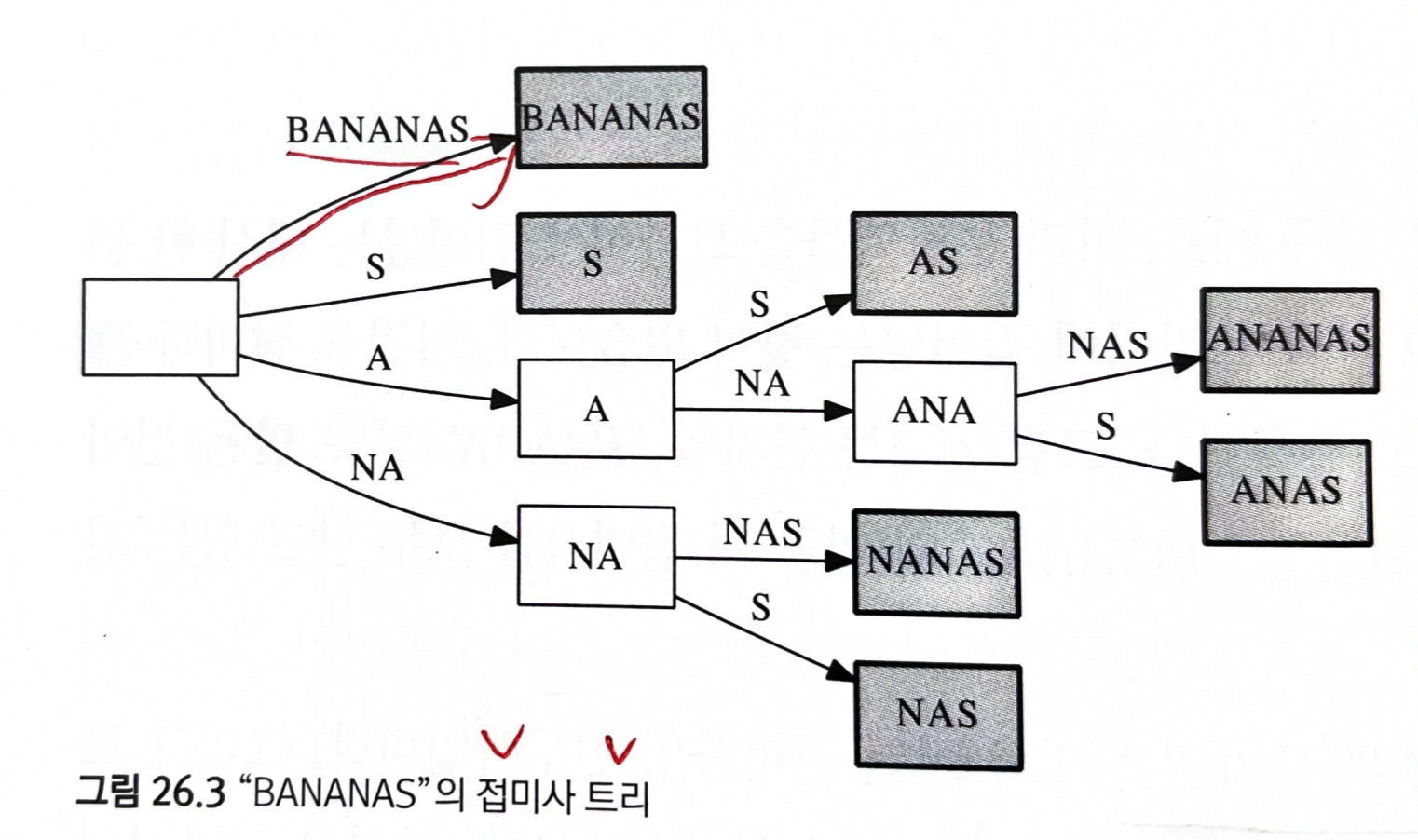
image-20240425150219073.png

  • 접미사 트리(suffix tree) 는 이 문제를 해결하기 위해 고안됨
    • 접미사 트라이의 많은 부분은 분기 없이 일자로 구성되어 있다는 것에 착안
    • 각 간선이 문자열의 한 글자가 아니라 여러 글자에 대응되도록 한다.
    • 실질적으로 트리 상 긴 일자 경로를 압축하는 효과

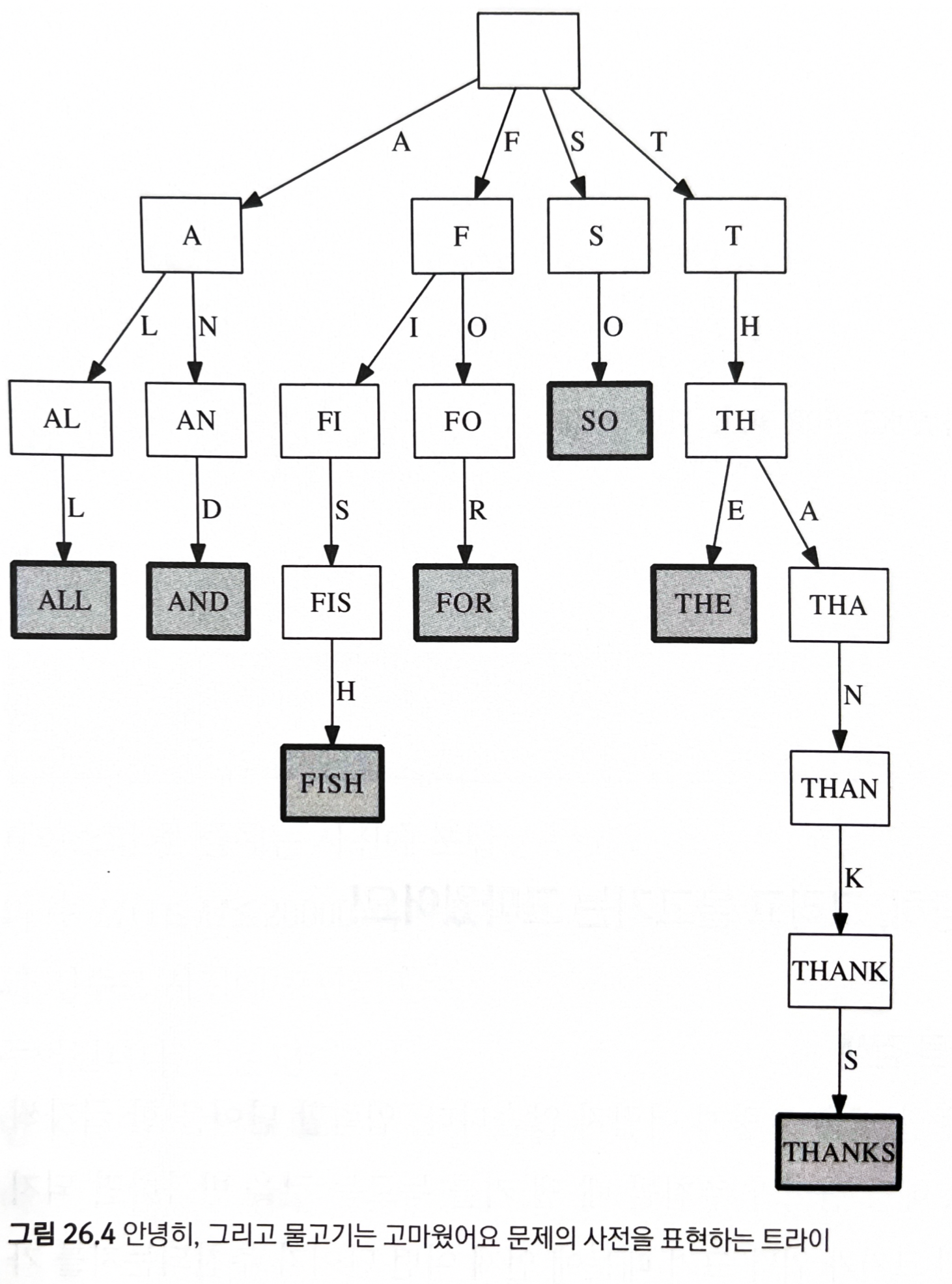
26.2, 26.3 안녕히, 그리고 물고기, SOLONG, 난이도: 중

image-20240425150250987.png

Reference