27. 그래프의 표현과 정의

27.1 도입

  • 그래프(graph)는 현실 세계의 사물이나 추상적인 개념 간의 연결 관계를 표현한다.
    • 트리에 있었던 부모 자식 관계에 관한 제약이 없기 때문에 그래프는 트리보다 다양한 구조를 표현할 수 있다.
    • 트리도 그래프 중 하나

27.1.1 그래프의 정의

  • 그래프 G(V, E)는 어떤 자료나 개념을 표현하는 정점(vertex, node)의 집합 V와 이들을 연결하는 간선(edge)들의 집합 E로 구성된 자료구조 이다.
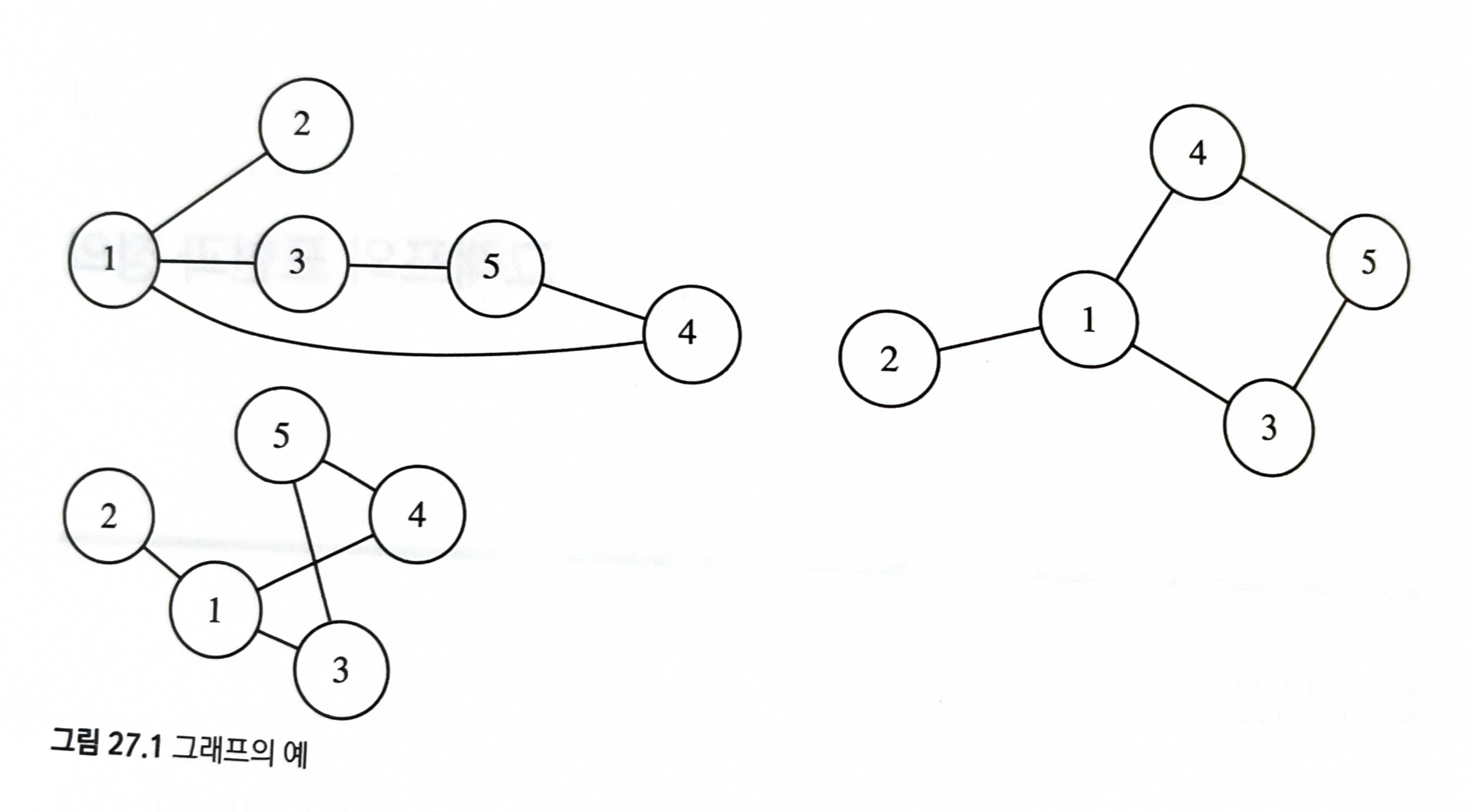
  • 그래프는 정점들과 간선들로 정의되며, 정점의 위치 정보나 간선의 순서 등은 그래프의 정의에 포함되지 않는다.
    • 아래 그래프들은 모두 같은 그래프를 표현한다.

image-20240418145926568.png

27.1.2 그래프의 종류

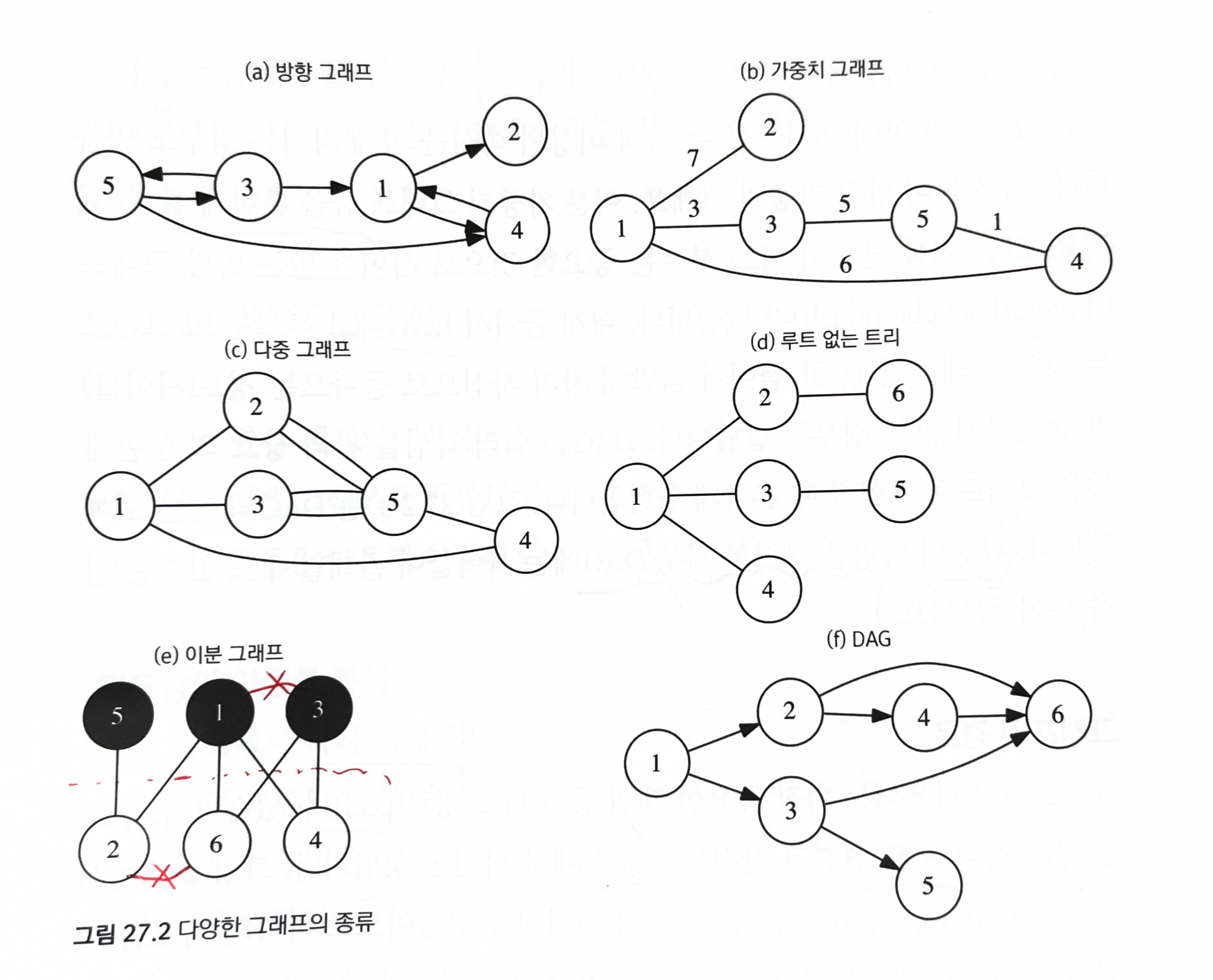
image-20240418150007436.png

  • 방향 그래프(directed graph) or 유향 그래프

    • 방향 그래프에서는 각 간선이 방향이라는 새로운 속성을 갖는다.
    • u -> v 와 v-> u 는 서로 다른 간선이다.

  • 무향 그래프

    • 간선에 방향이 없는 그래프

  • 가중치 그래프(weighted graph)

    • 각 각선에 가중치(weight)라고 불리는 실수 속성을 부여

  • 다중 그래프(multigraph)

    • 두 정점 사이에 두 개 이상의 간선이 있을 수 있는 그래프

  • 단순 그래프

    • 두 정점 사이에 최대 한 개의 간선만 있는 그래프

  • 트리 or 루트 없는 트리(unrooted tree)

    • 부모 자식 관계가 없을 뿐, 간선 들의 연결 관계만 보면 트리와 같은 무향 그래프를 말한다.
    • 간선들의 연결 관계가 트리와 같다는 말은, 간선을 통해 두 정점을 잇는 방법이 딱 하나밖에 없다는 의미

  • 이분 그래프(bipartite graph)

    • 그래프의 정점들을 겹치지 않는 두 개의 그룹으로 나눠서 서로 다른 그룹에 속한 정점들 간에만 간선이 존재하도록 만들 수 있는 그래프
    • Ex) 남성과 여성

  • 사이클 없는 방향 그래프(directed acyclic graph, DAG)

    • 방향 그래프인데, 한 점에서 출발해 자기 자신으로 돌아오는 경로(사이클) 가 존재하지 않는 경우
    • 간선의 방향을 무시할 경우 DAG에는 사이클이 존재할 수도 있다.

27.1.3 그래프의 경로

  • 경로(path): 끝과 끝이 서로 연결된 간선들을 순서대로 나열 한 것
    • 주로, 거쳐 가는 정점의 번호만을 간단히 써서 표기함
    • (1, 2), (2, 4), (4, 5) === 1 -> 4 -> 5
  • 방향 그래프의 경우 앞 간선의 끝점이 뒷 간선의 시작점과 만나야 한다
  • 경로 중 한 정점을 최대 한 번만지나는 경로를 단순 경로(simple path) 라고 한다.
  • 현대 그래프 이론에서는 ‘경로’ 라고 하면 대부분은 ‘단순 경로‘를 의미한다.
    • 한 정점을 두 번 이상 지날 수 있는 경로를 이야기 할 대는 별도로 이 사실을 명시한다.
  • 시작한 점에서 끝나는 경로를 사이클 라고 한다.
    • 사이클(cycle): 시작점과 끝나는 점이 같은 경로

27.2 그래프의 사용 예

  • 현실 세계의 수 많은 문제를 풀기 위해 그래프가 사용된다.
  • 철도망의 안전성 분석
  • 소셜 네트워크 분석
  • 인터넷 전송 속도 계산
  • 한 붓 그리기
    • 주어진 그래프의 모든 간선을 한 번씩만 지나는 경로: 오일러 경로(Eulerian path)
  • 외환 거래

27.3 암시적 그래프 구조들

  • 현실 세계에서 그래프 같은 형태를 갖는 구조가 아니라도 그래프를 통해서 표현하면 쉽게 해결 할 수 있는 문제

    • 이 같은 그래프 구조를 암시적 그래프(implicit graph) 라고 한다.
    • Ex) 2차원 board에서 미로 최단 경로 찾기

  • 할 일 목록 정리

    • 위상 정렬(topological sorting), DFS를 응용

  • 15-퍼즐

  • 게임판 덮기

  • 회의실 배정

    • 만족성 문제(satisfiability problem)
    • 모든 사람이 두 선택지 중 하나를 선택해야 하는 문제: 2-SAT 문제

27.4 그래프의 표현 방법

  • 많은 경우 그래프는 트리에 비해 정적인 용도로 사용된다.
    • 보다 정적이라는 말은 새로운 정점이나 간선을 추가, 삭제 하는 일이 자주 일어나지 않는다는 의미
    • 따라서 대부분의 그래프는 구조의 변경이 어렵더라도 좀 더 간단하고 메모리를 적게 차지하는 방법으로 구현된다.
  • 그래프의 정점(node)들을 객체의 인스턴스로 표현하는 대신(트리 방식), 각 정점에 0부터 시작하는 번호를 붙이고, 배열에 각 정점의 정보를 저장하는 것
  • 그래프의 표현 방식은 간선(edge)의 정보를 어떤 식으로 저장하는냐에 따라 크게 2가지로 나눈다.
    • 이 두 가지 방법은 표현 방법은 메모리나 시간 사용 특성이 굉장히 다르다.

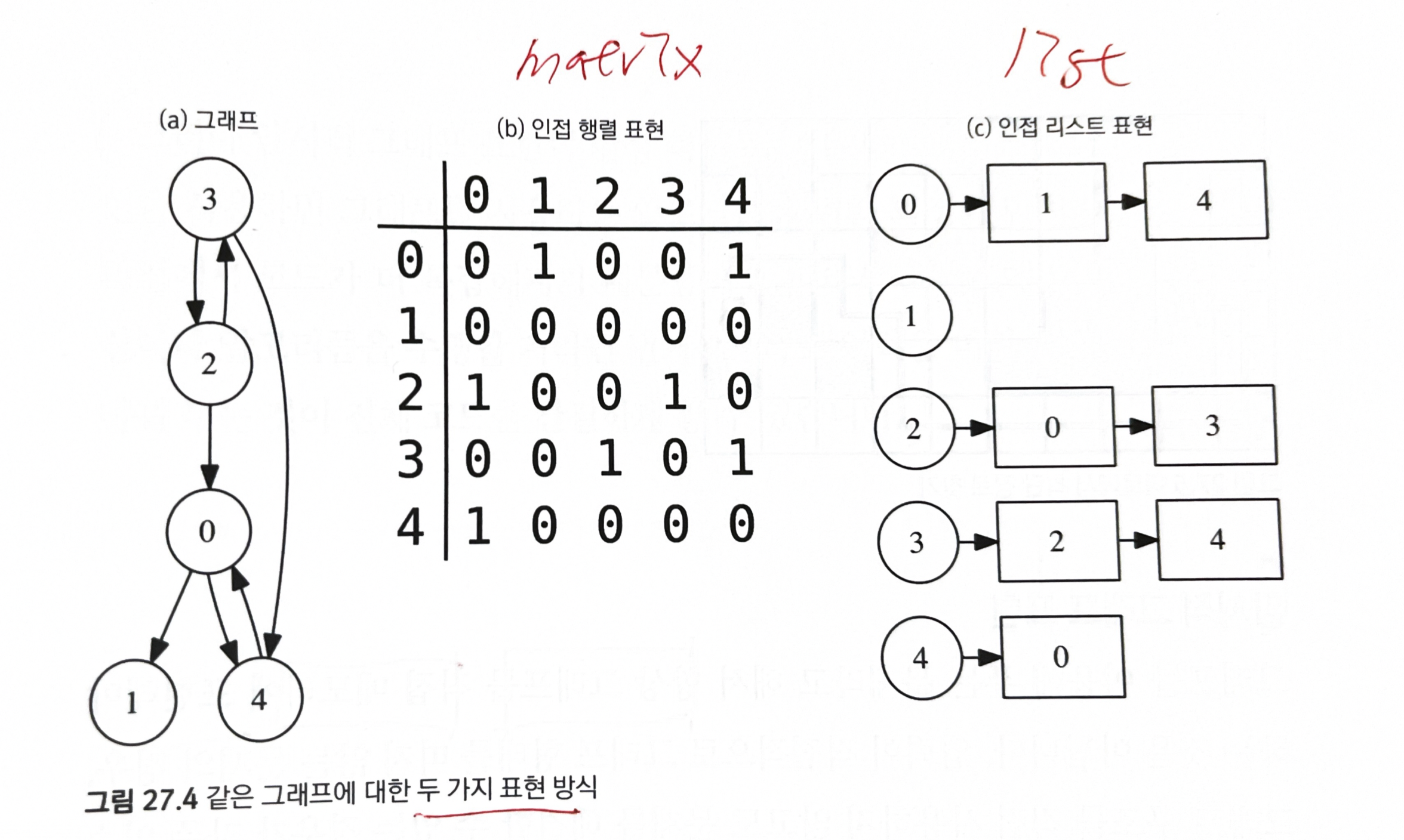
27.4.1 인접 리스트 (adjacency list) 표현

  • 그래프의 각 정점 마다 해당 정점에서 나가는 간선의 목록을 저장해서 그래프를 표현

  • 각 정점(node)마다 하나의 연결 리스트를 갖는 방식으로 구현

  • 노드 중심

  • adjacent[i]: 정점 i와 간선을 통해 연결된 정점들의 번호를 저장하는 연결 리스트

    • 실제로는 이 리스트에 정보를 추가, 삭제 할 일이 많지 않기 때문에 동적 배열을 사용해도 좋다

  • 무방향 그래프(Undirected Graph)에서 (a, b) 간선은 두 번 저장된다.

    1. 한 번은 a 정점에 인접한 간선을 저장하고 다른 한 번은 b에 인접한 간선을 저장한다.
    2. 정점의 수: N, 간선의 수: E인 무방향 그래프의 경우
    3. N개의 리스트, N개의 배열, 2E개의 노드가 필요
  • 0: 1
1: 2
2: 0, 3
3: 2
4: 6
5: 4
6: 5

  • 장점

    • O(V+E) 크기의 메모리 공간을 사용
    • 어떤 노드에 인접한 노드들을 쉽게 찾을 수 있다.

  • 단점

    • 간선 (u, v)가 존재하는 확인하기 위해서는 연결 리스트 (adjacent[i])를 처음 부터 읽어가면서 각 원소를 일일이 확인해야 한다
    • 간선의 존재 여부와 정점의 차수: 정점 i의 리스트에 있는 노드의 수 즉, 정점 차수만큼의 시간이 필요

27.4.2 인접 행렬(adjacency matrix) 표현

  • 인접 리스트 표현의 큰 단점은 두 정점이 주어질 때 이 정점이 연결되어 있는 지를 알기 위해서는 연결 리스트를 일일이 뒤져야 한다는 것

  • 이와 같은 연산의 속도를 높이기 위해 고안된 그래프 표현 방식이 인접 행렬이다.

  • 그래프의 인접 행렬은 이름에서 유추할 수 있듯이 |V|x|V| 크기의 행렬 (2차원 배열)을 이용해 간선의 정보를 저장한다.

  • adjacent[i][j]: 정점 i에서 정점 j로 가는 간선이 있는지를 나타내는 boolean 값 변수

  • 가중치 그래프를 인접 행렬로 표현하려면 각 간선의 정보를 boolean 이 아니라, 정수, 실수(가중치 값)로 두면 된다.

    • 두 정점 사이에 간선이 없는 경우 -1 or inf 로 지정한다.

  • 무방향 그래프를 인접 행렬로 표현한다면 이 행렬은 대칭 행렬(Symmetric Matrix) 이 된다.

    • 물론 방향 그래프는 대칭 행렬이 안 될 수도 있다
  • 1
2
3
4

    if (간선 (i, j)가 그래프에 존재):
	matrix[i][j] = 1;
else
	matrix[i][j] = 0;

  • 장점

    • 정점의 번호 u, v가 주어졌을 때, 두 정점을 잇는 간선이 있는지를 한 번의 배열 접근만으로 확인 가능
    • 정점의 차수 는 O(V) 안에 알 수 있다: 인접 배열의 i번 째 행 또는 열을 모두 더한다.

  • 단점

    • 실제의 간선의 개수와 관계없이 항상 O(V^2) 크기의 메모리 공간을 사용
    • 어떤 노드에 인접한 노드들을 찾기 위해서는 모든 노드를 전부 순회해야 한다.
    • 그래프에 존재하는 모든 간선의 수는 O(V^2) 안에 알 수 있다. : 인접 행렬 전체를 조사한다.

27.4.3 인접 행렬 vs 인접 리스트

  • 서로 완전히 정반대의 특성을 가져서, 한 방식의 단점이 바로 다른 방식의 장점이다.
  • 따라서, 알고리즘, 그래프의 종류에 따라서 2가지 중 적절히 선택해야 한다.
  • 간선의 수가 V^2 에 비해 훨씬 적은 그래프를 희소 그래프(sparse graph) 라고 한다.
    • 인접 리스트를 사용하는 것이 유리
  • 반대로, 간선의 수가 거의 V^2에 비례하는 그래프를 밀집 그래프(dense graph) 라고 한다.
    • 인접 행렬을 사용하는 것이 유리

image-20240418145902070.png

27.4.4 에지 리스트(Edge List)

  • 간선, edge를 중심으로 그래프를 표현
  • 에지 리스트는 리스트에 출발 노드, 도착 노드를 저장하여 Edge를 표현
  • 또는 출발 노드, 도착 노드, 가중치를 저장
  • MST, 벨만-포드, 크루스칼에 주로 사용
  • 노드 중심 알고리즘에는 잘 사용하지 않음.
  • edgeLst = [ (1,2,8), (1,3,3), (3,4,13), (2,4,4), (2,5,15), (4,5,2) ] # 출발, 도착, 가중치

27.4.5 암시적 그래프 표현

  • 그래프를 이용해 푸는 문제라고 해서, 항상 그래프를 직접 메모리에 표현해야 하는 것은 아니다.

  • 암시적 그래프로 표현 가능

    • 2차원 board에서 미로 최단 경로 찾기
      • 각 빈칸을 정수 일렬번호를 갖는 정점으로 표현하는 대신, 빈 칸의 위치 (y, x) 로 표현 할 수 있다
      • 주어진 입력을 그래프로 변환하는 번거로운 과정을 거칠 필요 없이 BFS 가능
    • 15-퍼즐
      • 모든 상태(16!===20조) 를 그래프로 표현하는 것은 실용적인 방법이 아니다.

  • 암시적 그래프 표현이 항상 더 좋은 것은 아니다.

    • 그래프 사용 알고리즘과 변환 과정이 합쳐지게 되면 더 복잡해 질 수 도 있다.

    • 번거롭더라도 입력을 미리 그래프 표현으로 바꿔 두는 것이 전체 코드를 더 간결하게 할 수 있다.

Reference