29. 그래프의 너비 우선 탐색
29.1 도입
28.1.1 너비 우선 탐색(Breadth First Search)
너비 우선 탐색은 시작점에서 가까운 정점(Node)부터 순서대로 방문하는 탐색 알고리즘
시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘
각 정점을 방문할 때 마다 모든 인접 정점들을 검사
이 중 처음 보는 정점을 발견하면, 이 정점을 방문 예정이라고 기록, 큐에 저장
너비 우선 탐색의 방문 순서는 정점을 먼저 꺼내는지에 의해 결정
이를 구현하는 방법은 목록에 먼저 넣은 정점을 항상 먼저 꺼내는 것
정점 목록을 큐(queue) 를 사용하면 너비 우선 탐색의 조건을 만족시킬 수 있다.
- 그래서 큐(queue) 를 쓰는 거다
그래프의 너비 우선 탐색 python 구현
- DFS의
visited[]가 각 정점의 방문 여부를 저장했던 것에 비해, - BFS에서
discovered[]는 각 정점의 발견 여부를 저장한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15discovered = [False for _ in range(N)] result = [] def bfs(startNode): q = deque([ [startNode] ]) discovered[startNode] = True while q: node = q.popleft() result.append(node) for nxt in graph[node]: if not discovered[nxt]: q.append(nxt) discovered[nxt] = True- DFS의
DFS와 달리 BFS에서는 발견(discover) 과 방문(visit) 이 같지 않다.
모든 정점은 다음 3개의 상태를 순서대로 거쳐 간다.
- 아직 발견되지 않은 상태 (visited = False)
- 발견되었지만 아직 방문되지 않은 상태 (in queue)
- 방문된 상태 (discoverd = True)
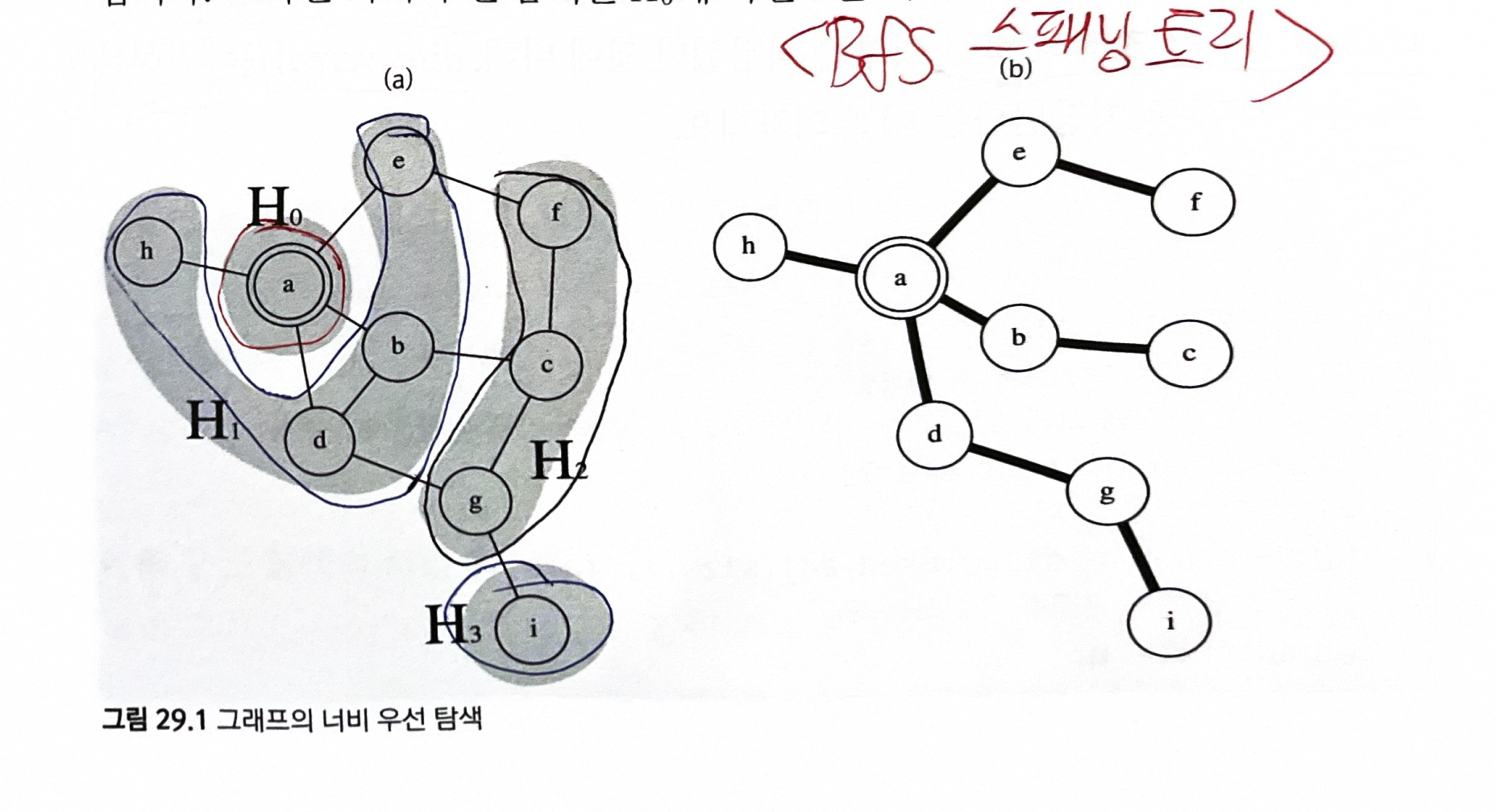
BFS에서 새 정점을 발견하는데 사용했던 간선들을 모은 트리를
BFS 스패닝 트리(BFS Spanning Tree)라고 한다.
29.1.2 너비 우선 탐색의 시간 복잡도
- DFS와 다를 게 없다.
- 모든 정점을 한 번씩 방문하며, 정점을 방문할 때마다 인접한 모든 간선을 검사한다
- 인접 리스트 인 경우: O(V+E)
- 인접 행렬 인 경우: O(V^2)
29.1.3 너비 우선 탐색과 최단 거리
- 그래프의 구조에 관한 다양한 문제를 푸는 데 사용되는 DFS와 달리, BFS는 대게 딱 하나의 용도로 사용된다.
- 바로 그래프의 최단 경로 문제를 풀 때 사용
- BFS를 간단하게 변경해 모든 정점에 대해 시작점으로 부터의 거리 distance[]를 계산할 수 있기 때문이다.
- 시작점 부터 v까지의 최단 거리
distance[v]는distance[u] + 1이다.- 간선 (u, v)를 처음 발견해 큐에 넣었다고 가정할 때
- 시작점으로부터 다른 모든 정점까지의 최단 경로를 BFS 스패닝 트리 위에서 찾을 수 있다.
- 시작점으로 부터의 최단 경로는 ‘BFS 스패닝 트리에서 루트로 가는 경로’
29.1.4 모든 점의 발견
- 그래프 전체 구조에 관한 정보를 얻기 위해 사용되는 DFS와 달리,
- BFS는 대게 시작점으로부터 다른 정점들까지의 거리를 구하기 위해 사용된다.
- 따라서, DFS 처럼 모든 정점을 검사하면서 수행하는 작업 BFS는 잘하지 않는다.
29.2, 29.3 Sorting Game, SORTGAME, 난이도: 중
| |
- 문제를 읽고, 그래프로 접근, 바꾸기
{3, 4, 1, 2} === {9, 100, 5, 6}상대적 크기가 같음- 모든 상태를 미리 BFS를 통해 계산
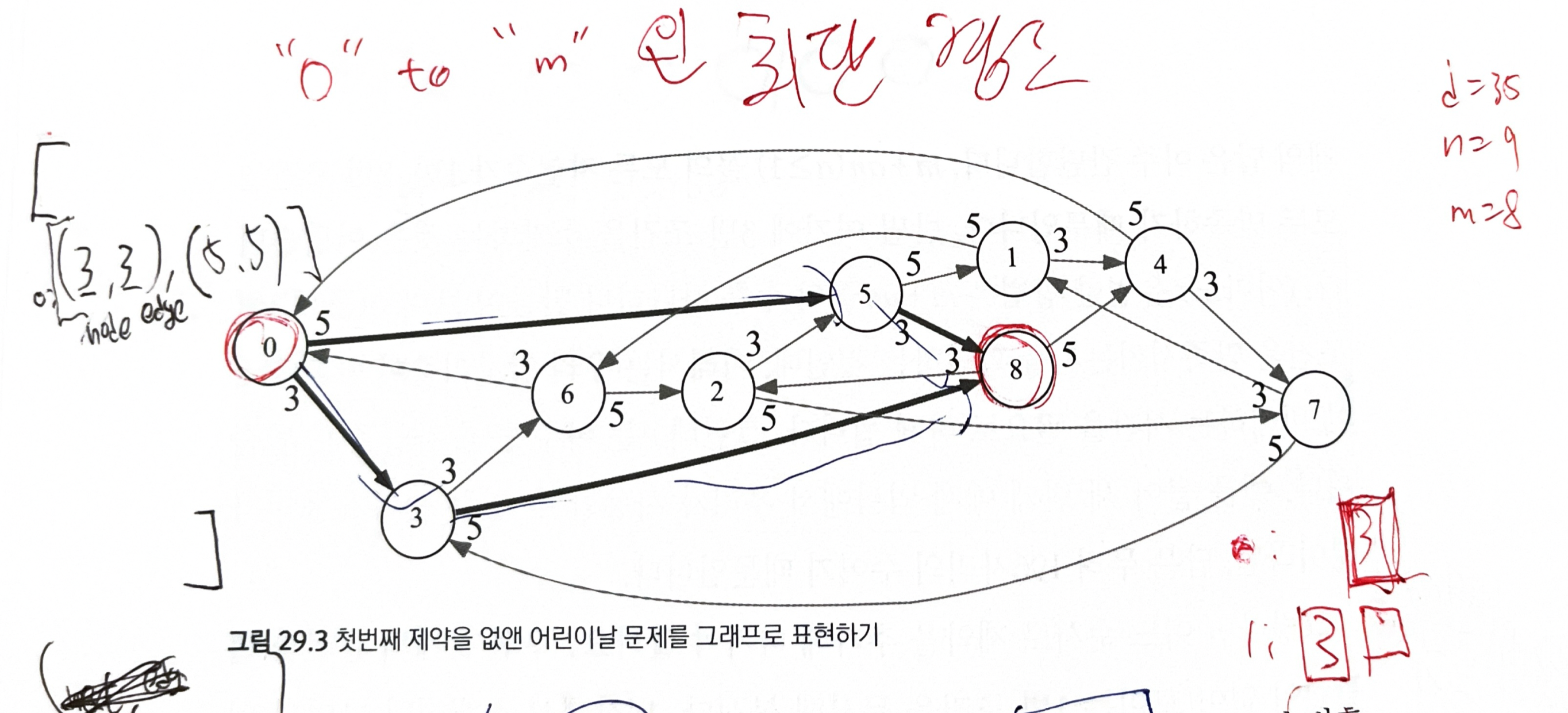
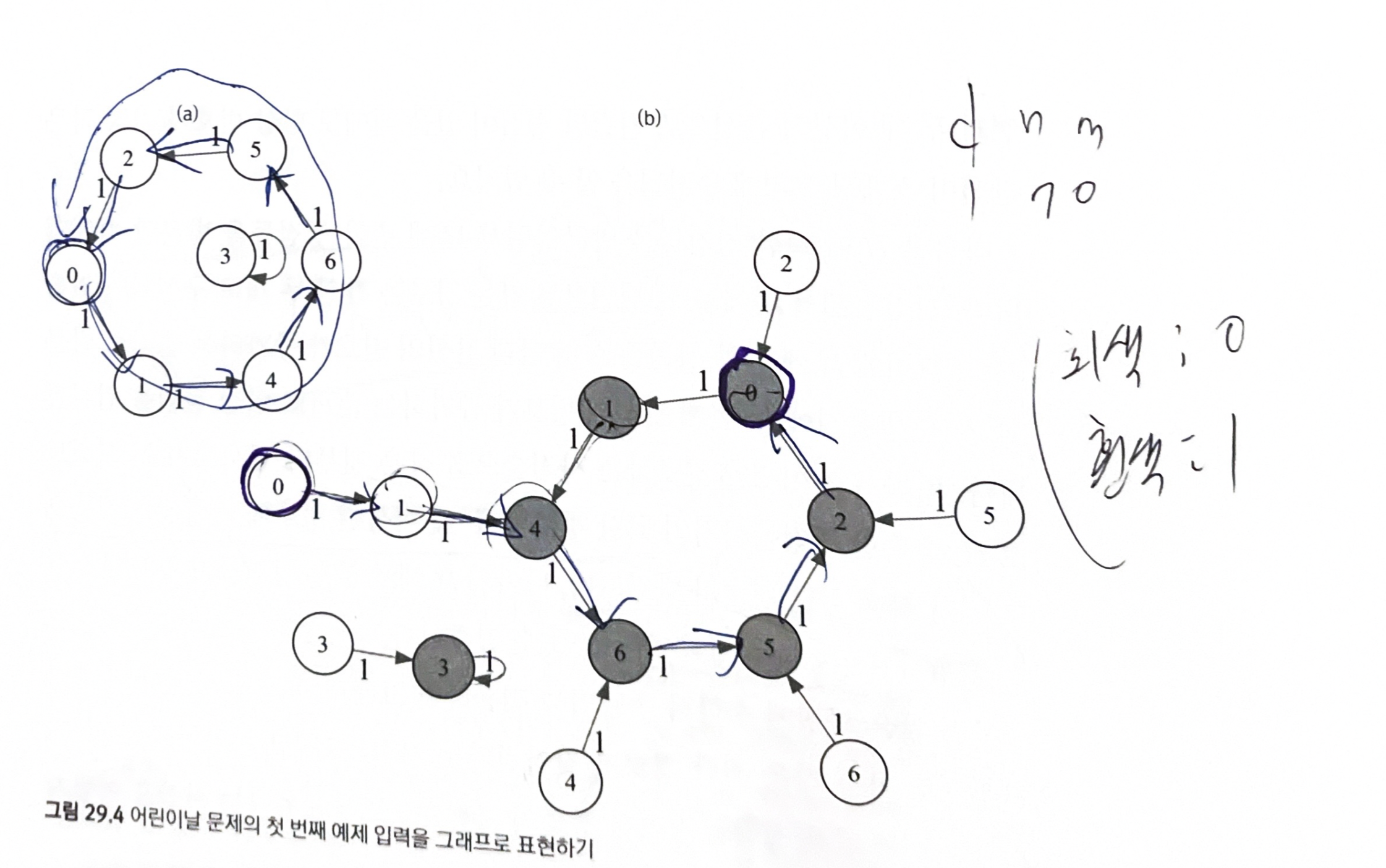
29.4, 29.5 어린이날, CHILDRENDAY, 난이도: 상
| |
- 여러 개의 조건이 있는 문제
- 일부 조건을 없앤 더 단순한 문제를 푼 후, 조건을 하나하나 추가
- mod 연산, 법칙
- 사전순으로 가장 최단 경로 => 임의의 순서 대신 번호가 증가하는 순서(오름 차순)으로 검사
- 조건 강제
29.6 (기본 BFS 말고) 최단 경로 전략
게임판의 상태를 그래프로 표현: 상태 공간(state space)
- 15-퍼즐 문제는 그래프상의 최단 경로 문제로 변경
- 상태 공간을 전체 탐색하지 않고, 답을 찾는 데로 BFS를 종료하기 때문에 시간 복잡도를 다르게 계산해야 한다.
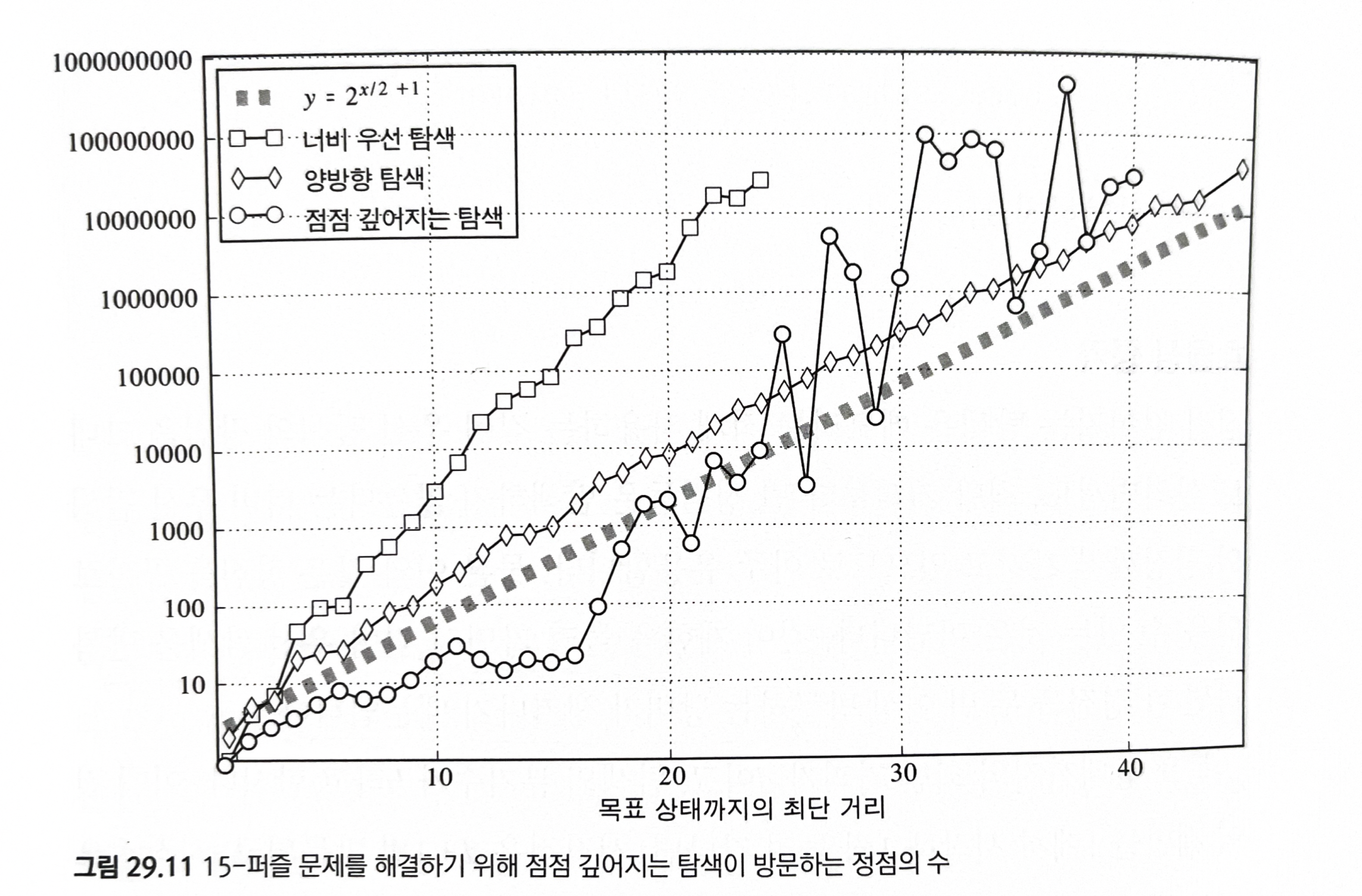
- 너브 우선 탐색이 방문하는 정점의 개수에 가장 직접적인 영향을 주는 요소는 최단 거리 d 이다.
- 방문하는 정점의 개수에 영향을 미치는 다른 요소는 탐색의 분기 수(branching factor) b 이다.
- 방문하는 정점의 수: O(b^d) 지수적으로 증가
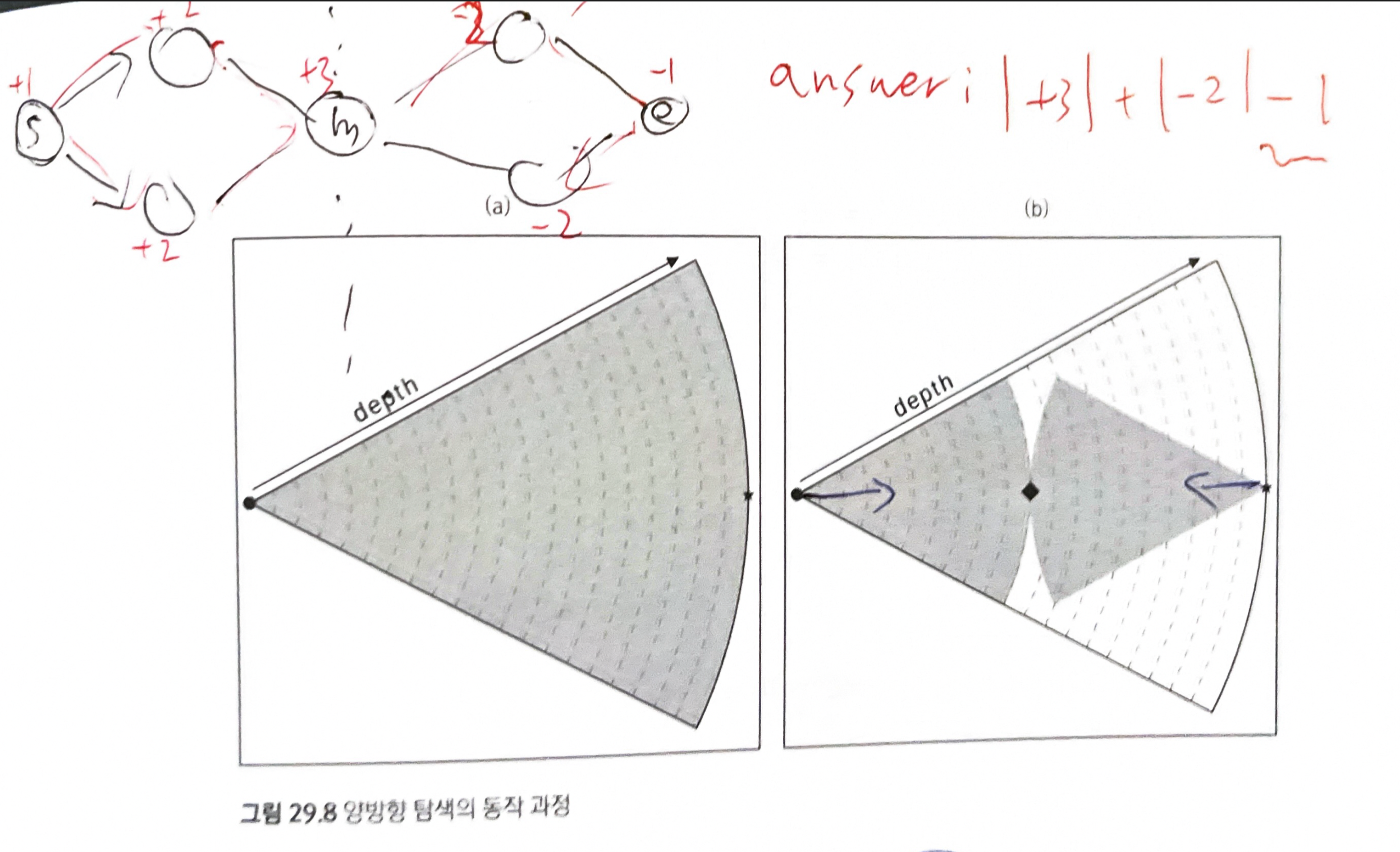
29.6.1 양방향 탐색(bidirectional search)
- 시작 정점에서 시작하는 정방향 탐색과, 목표 정점에서 시작해 거꾸로 올라오는 역방향 탐색을 동시에 하면서, 이 둘이 가운데서 만나면 종료
- 정방향과 역방향 탐색에서 방문할 정점들을 모두 같은 큐에 넣음
- 최단 거리를 저장할 때는 정방향은 양수, 역방향은 음수로 저장 (구분하기 위해)
- 인접한 상태를 검사했는데, 서로 부호가 다르면, 가운데서 만났다는 의미
- 목표 상태에서 역방향으로 움직이기 쉬워야 가능 함
29.6.2 점점 깊어지는 탐색
양방향 탐색에서도 방문하는 정점 수는 최단 거리에 따라 지수적으로 증가, O(b^d/2)
따라서, 규모가 큰 탐색 문제를 풀 때는 DFS를 기반으로 한 방법을 사용해야 함
- DFS는 방문할 정점의 목록을 유지하는 BFS와 달리 정점을 발견하는 즉시 방문
- 큐가 너무 많은 메모리를 차지하는 일이 발생하지 않음
그러나 최단 경로를 찾기 불가능
- DFS는 목표 상태를 찾아도 지금까지 찾은 경로가 최단 경로인지 확신할 수 없다.
- 각 정점을 방문하지 않으면 한 상태를 두 번 방문할 수 도 있고, 사이클에 빠져 탐색이 종료하지 않을 수 있다.
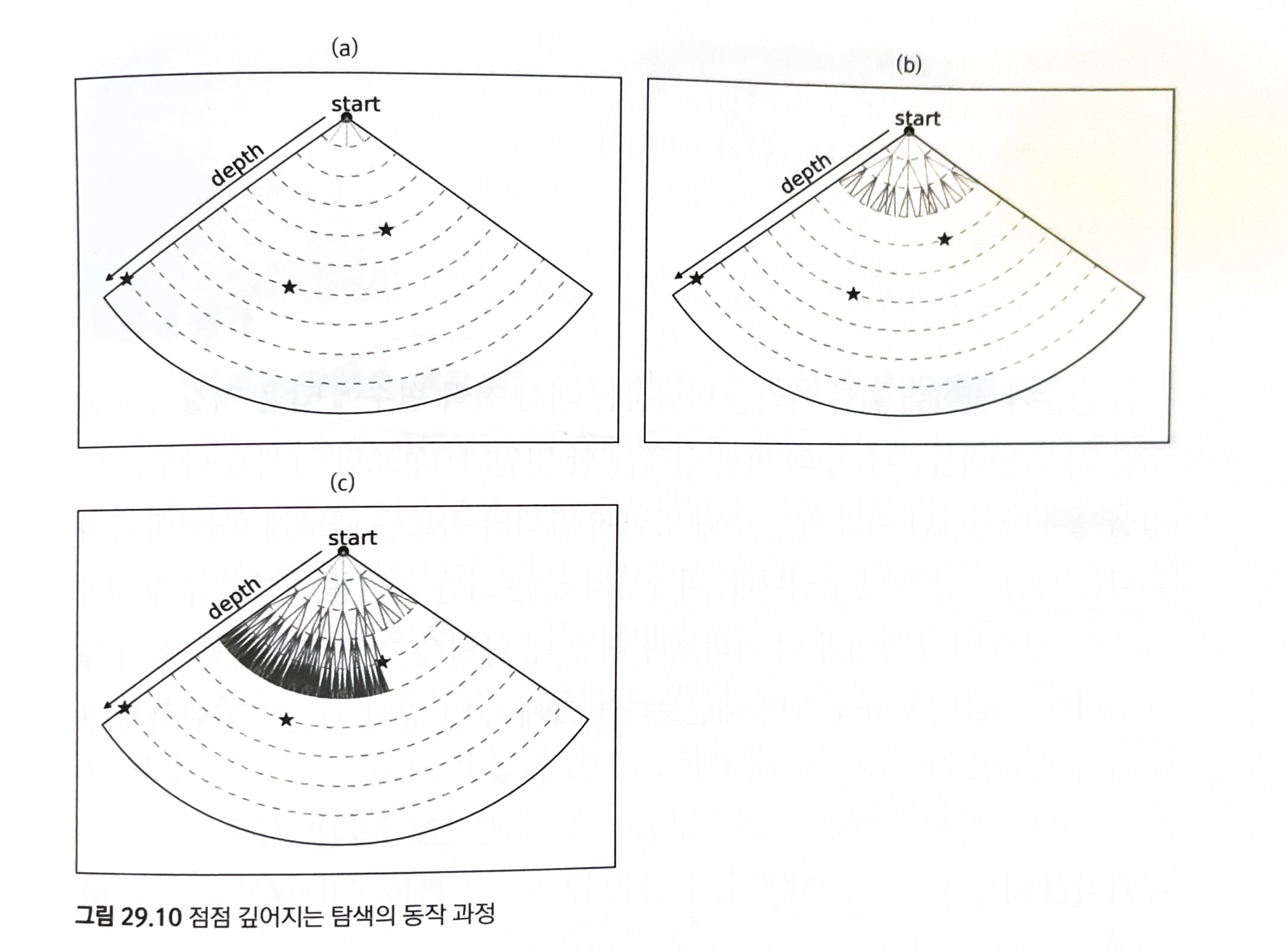
IDS(Iteratively Deepening Search, 점점 깊어지는 탐색)이 이 문제를 해결하기 위해 고안됨임의의 깊이 제한 limit 보다 짧은 경로가 존재하는 DFS로 확인
- 답을 찾으면 성공이니 반환
- 찾지 못하면, limit 을 늘려서 다시 시도
IDS는 조합 탐색(가지치기) 와 관계가 깊다.
- 깊이 제한을 늘려가면서 DFS를 반복하면 한 정점을 두 번 이상 방문하는 낭비가 생겨난다.
- 방문하는 상태의 수 O(b^d)
- IDS는 큐를 사용하지 않기 때문에, 메모리는 스택만 사용함
- 최대 메모리 사용량은 탐색의 깊이에 비례하게 된다. O(d)
29.6.3 탐색 방법 선택하기
- 최단 경로 찾는 경우, BFS를 우선 고려
- 메모리 사용량, 탐색의 깊이 한계 확인
- 양방향 탐색 고려, 목표 상태에서 역방향으로 움직이기 쉬워야 함
- IDS 고려
29.6.4 상태 객체의 구현
- 상태에 대한, 여러 연산을 가능한 한 효율적으로 구현
- 가능한 한 적은 메모리 사용
- 비트마스크 기법
- 일대일 대응 함수
- 현재 상태가 몇 번째인지 계산하는 일대일 함수를 작성하면, 현재 상태를 정수로 표현 가능
29.7, 29.8 하노이의 탑, HANOI4B, 난이도: 중
- start state —–bfs for find 최단 경로—-> end state
- 시작과 끝 상태가 유일하게 정해져 있음, 그래프가 양방향 그래프 이기 때문에 양방향 탐색ㅇ글 적용하기 용이하다.
| |
Reference
- 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 (구종만, 인사이트)
- https://www.algospot.com/