30. 최단 경로 알고리즘

30.1 도입

최단 경로 문제(shortest path problem)은 주어진 그래프에서 주어진 두 정점을 연결하는 가장 짧은 경로의 길이를 찾는 문제
가중치가 없는 그래프(가중치가 모두 1인)에 대한 최단 경로는 BFS로 찾을 수 있다.
‘최단 경로를 구성하는 정점들의 목록’을 구해 주는 것이 아니라 최단 경로의 길이를 찾아 줄 뿐이다.
실제 경로를 계산하기 위해서는 BFS에서 그랬듯이 탐색 과정에서 별도의 정보를 저장하고, 이것으로 실제 경로를 찾아내는 과정을 구현해야 한다.
다양한 그래프의 종류와 특성에 따라 최적화된 많은 최단 경로 알고리즘이 존재한다.

30.1.1 음수 간선의 중요성

음수 가중치를 갖는 간선(음수 간선) 이 있는지의 여부가 중요
당연하지만, 음수 간선을 지나가면 전체 경로의 길이가 짧아 진다.
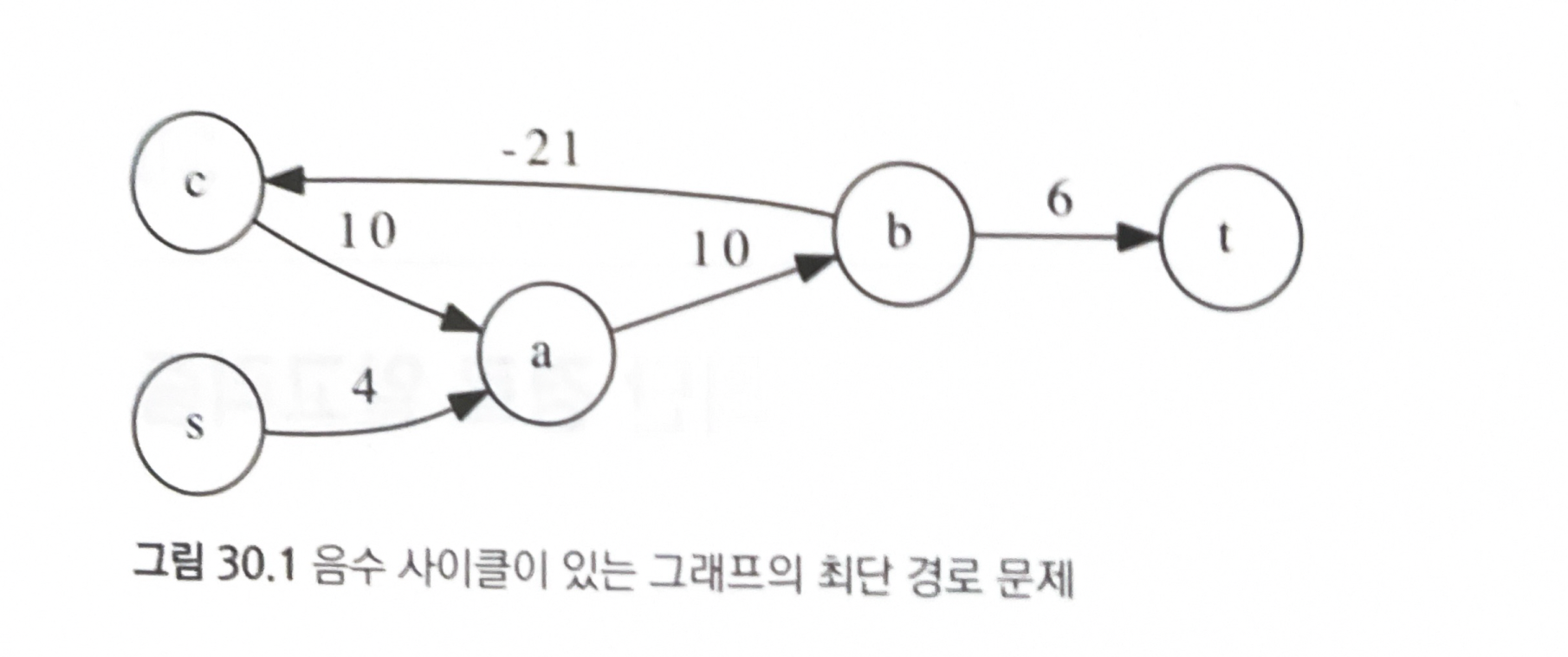
가중치의 합이 음수인 사이클(음수 사이클) 이 등장할 수 있다.
음수 사이클이 있는 경우 최단 경로 문제는 제대로 정의되지 않는다.
음수 사이클이 있는 그래프에서는 어떤 최단 경로 알고리즘도 최단 경로를 정확하게 찾을 수 없다.
알고리즘에 따라 음수 사이클이 있다는 것을 확인할 수 있다 (벨만-포드 알고리즘)

30.1.2 단일 시작점과 모든 쌍 알고리즘

단일 시작점 알고리즘과 모든 쌍 알고리즘 으로 나뉜다.
모든 쌍 알고리즘의 수행 결과는 V x V 크기의 2차원 배열이 된다.
- 이 배열의 각 원소는 두 정점 사이의 최단 거리를 나타낸다.
- 대표적인 플로이드-워셜 알고리즘이 있다.

30.1.3 방향 그래프와 무방향 그래프

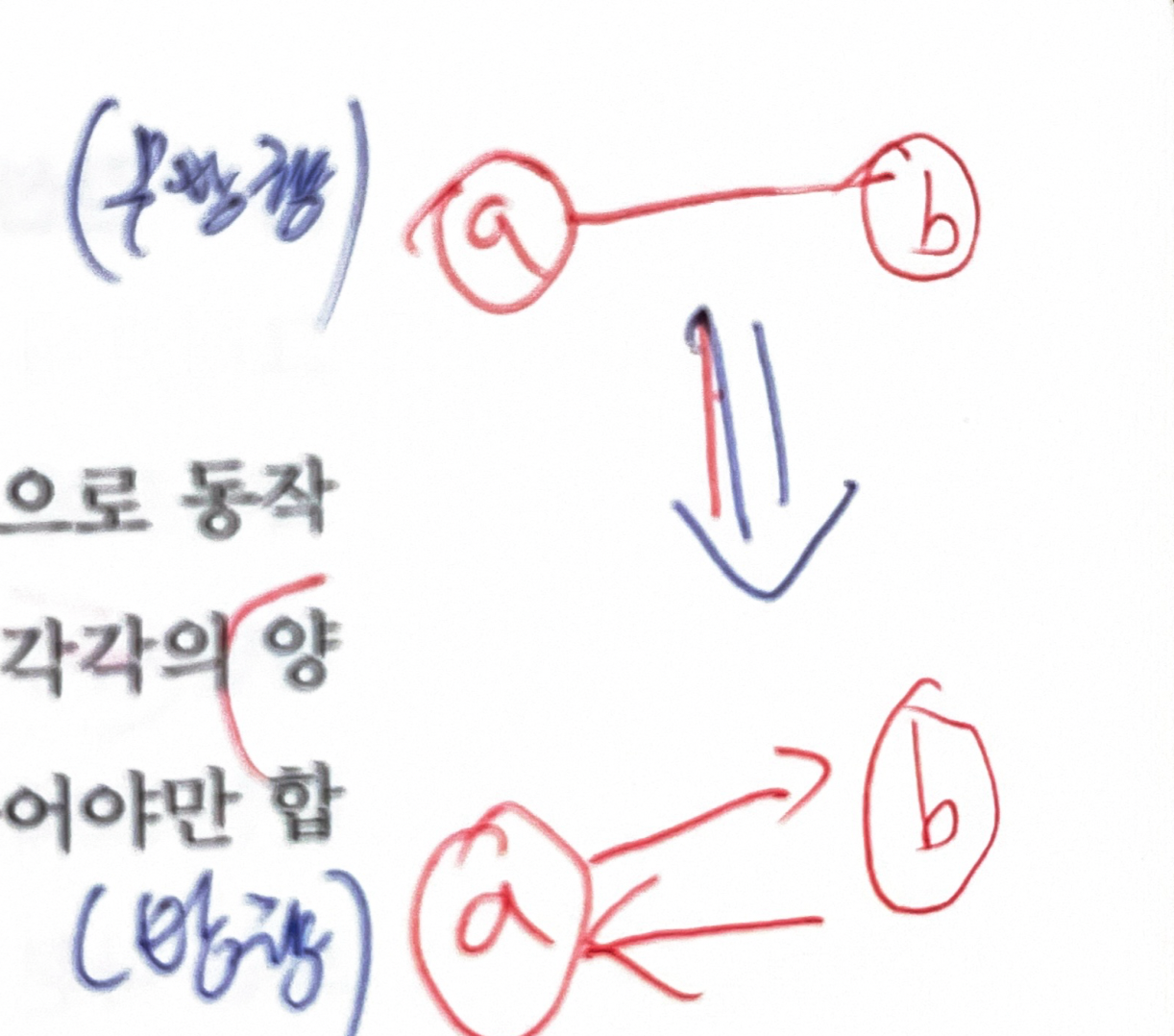
최단 거리 알고리즘들은 모두 방향 그래프를 기준으로 동작
무방향 그래프에서 최단 경로를 찾기 위해서는 양방향 간선을 두 개의 일반 통행 간선으로 쪼개서, 방향 그래프로 만들어야 한다
- 음수 가중치가 있는 무방향 그래프는 음수 사이클이 생겨서 불가능하다.

30.2 다익스트라의 최단 경로 알고리즘

다익스트라 알고리즘은 단일 시작점 최단 경로 알고리즘이다. 시작 정점 s 에서 다른 모든 정점들까지의 최단 거리를 계산한다.

30.2.1 우선순위 큐를 사용하는 너비 우선 탐색

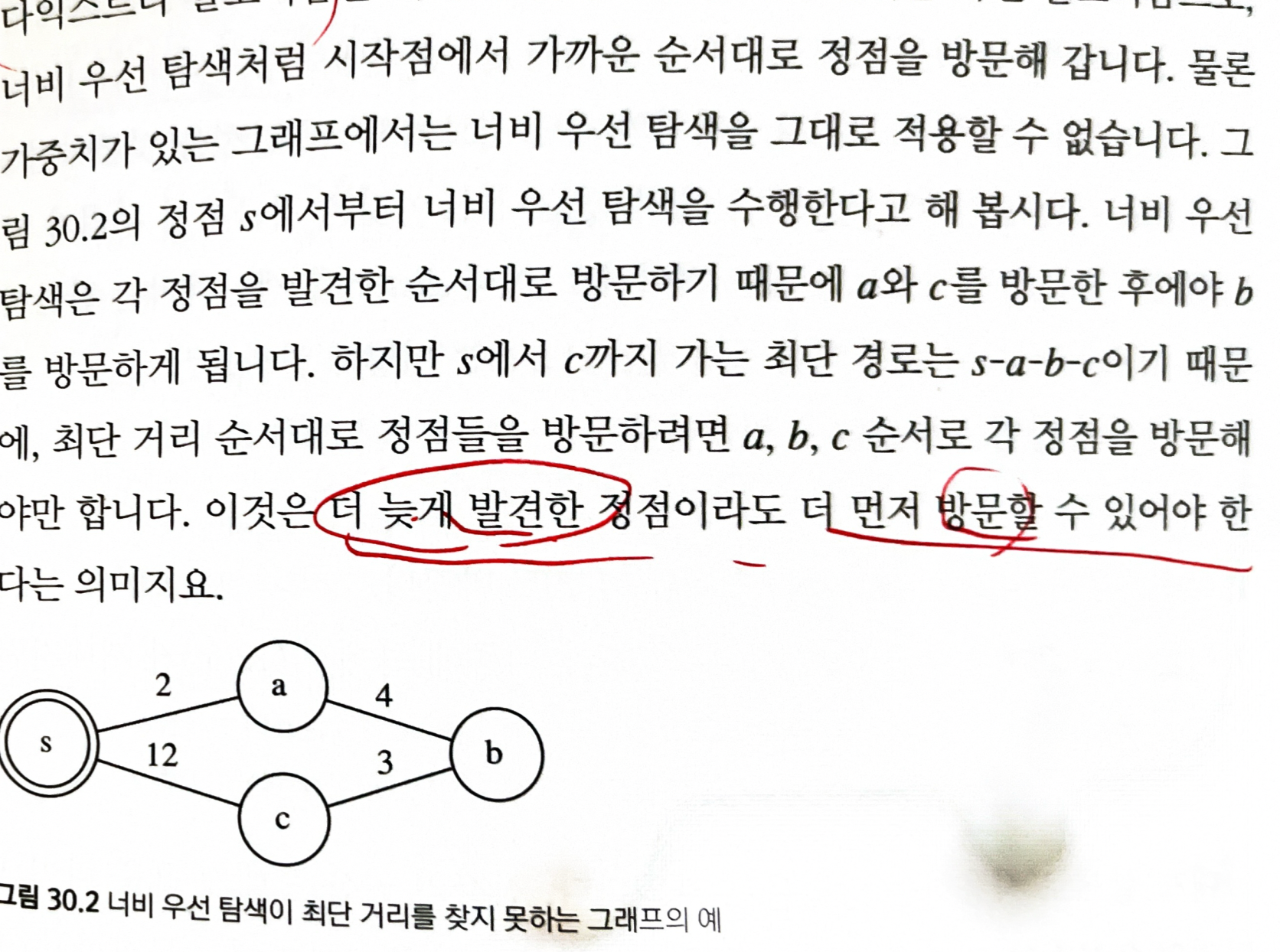
핵심: 더 늦게 발견한 정점이라도 더 먼저 방문할 수 있어야 한다.
- 큐 대신 우선순위 큐를 사용해서 이 문제를 해결
우선순위 큐에 정점의 번호와 함께 지금까지 찾아낸 해당 정점까지의 최단 거리를 쌍으로 넣는다.
우선순위 큐는 최단 거리를 기준으로 정점을 배열함으로써, 아직 방문하지 않은 정점 중 시작점으로 거리가 가장 가까운 정점을 찾는 과정을 간단히 해준다.
각 정점까지의 최단 거리를 저장하는 1차원 배열 dist[]를 유지하며, 정점을 방문할 때 마다 인접한 정점을 모두 검사
각 정점까지의 최단 경로가 갱신될 수 있다.
(9, c)는 dist[c]에 갱신하는 것은 간단하지만 이때, 이미 우선순위 큐에 들어있는 정보(12, c)는 어떻게 처리할까?
1. 우선순위 큐 내에서 (12, c)를 찾아내 (9, ㅊ)fh qkRnsek.
2. (12, c)를 그대로 두고, (9, c)를 추가한 뒤, 나중에 큐에서 (12, c)가 꺼내지면 무시한다.
보통 2번의 방법을 많이 사용한다. 1번은 우선순위 큐에서 지원하지 않을 뿐더러 직접 구현하기 복잡하다..
2번의 방법을 사용한다면, (12, c)를 무시해야 하는지 어떻게 알 수 있을까?
- dist[u]와 cost를 비교
- dist[u] < cost라면, u까지 오는 cost보다 짧은 경로가 이미 발견됐다는 의미임으로 (cost, u) 쌍은 무시하면 된다. -> continue 문
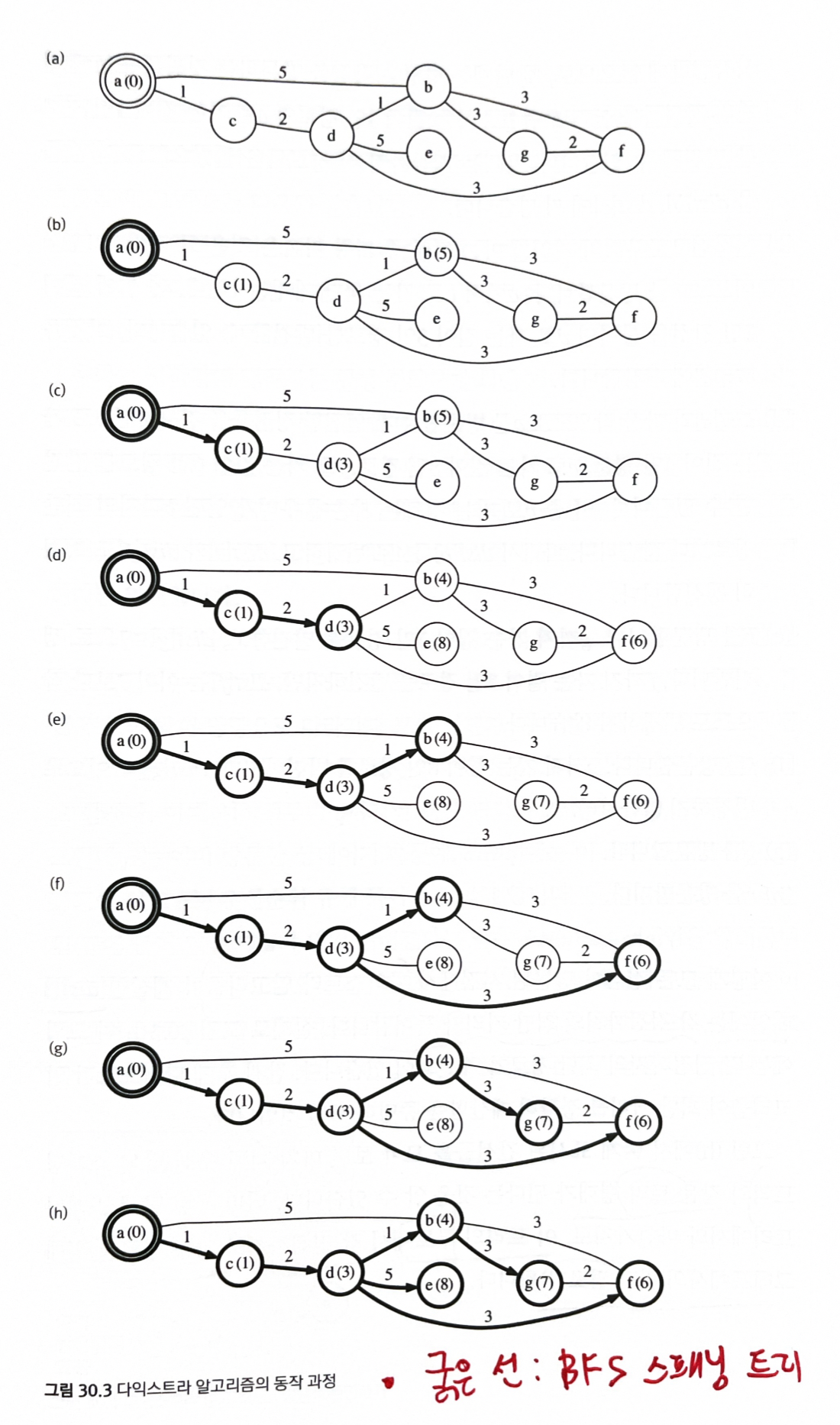
다익스트라 알고리즘이 계산한 dist[] 1차원 배열에는 각 정점까지의 최단 거리가 들어가 있다.
BFS 스패닝 트리와 마찬가지로, 이 트리의 루트에서 각 정점까지로 가는 경로는 원래 그래프에서의 최단 경로가 된다.
모든 간선의 가중치가 0 이상일때, 다익스트라 알고리즘이 정당하다.
- 음수 간선이 있는 그래프는 정답을 계산 못함

30.2.2 실제 구현 (python 코드)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from heapq import *

n, m = map(int, input().split())
INF = int(1e9)
start = int(input())
graph = [[] for i in range(n)]
distance = [float('inf') for _ in range(n)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))

def dijkstra(startNode):
    q = []
    heappush(q, (0, startNode))
    distance[startNode] = 0

    while q:  # 큐가 비어 있지 않다면
        curCost, node = heappop(q)

        if distance[node] < curCost:  # 만약 지금 꺼낸 것보다 더 짧은 경로를 알고 있다면 지금 꺼낸 것을 무시
            continue

        for nxt, weight in graph[node]:
            nCost = curCost + weight
            if nCost < distance[nxt]: # 더 짧은 경로를 발견하면, dist를 갱신하고 우선수위 큐에 넣는다.
                distance[nxt] = nCost
                heappush(q, (nCost, nxt))

30.2.3 다익스트라 시간 복잡도

수행 시간은 크게 두 부분
1. 강 정점마다 인접한 간선들을 모두 검사하는 작업: O(E)
2. 우선순위 큐에 원소를 넣고 삭제하는 작업: O(ElgE)
우선순위 큐에 최대 크기는 O(V)
- 그러나 dist[]를 갱신할 때마다 원소를 우선순위 큐에 넣기 때문에 그보다 많은 원소들이 들어갈 수 있다.
- 최악의 경우, 그래프의 모든 간선이 검사될 때마다 dist[]가 갱신되고, 우선순위 큐에 정점의 번호가 추가되는 것
추가는 각 간선마다 최대 한번 일어나기 때문에, 추가되는 원소의 수는 최대 O(E)
- 추가 삭제에 O(lgE)의 시간이 걸림
- 추가 삭제 전체 시간 복잡도: O(ElgE)
따라서, 1, 2번을 더하면 O(ElgE)d가 된다
- 대게 E는 V^2보다 작기 때문에, O(lgE) === O(lgV)
- 따라서, 최종 시간복잡도는 O(ElgV) 가 된다.

30.2.4 실제 경로 찾기

다익스트라는 최단 거리만을 계산할 뿐, 실제 경로를 찾으려면, 그래프를 탐색하는 과정에서 스패닝 트리를 계산한 후,
스패닝 트리를 거슬러 올라겨며 경로를 찾는 함수를 작성해야 한다.

30.2.5 O(VlgV)에 다익스트라 구현하기

중복 원소를 우선순위 큐에 넣지 않도록 수정하면 O(VlgV) 에 동작하도록 구현할 수 있다.
그러나 실제로는 이런 식의 코드를 작성하지 않는다.
피보나치 힙이나, 이진 검색 트리를 이용해 우선순위 큐를 작성해야 하는데,
- 이 같은 자료 구조들은 시간복잡도를 줄여 주지만, 구현이 복잡하거나 실제로 작성해서 속도를 측정하면 더 느린 경우가 많기 때문이다.

30.2.6 우선순위 큐를 사용하지 않는 다익스트라의 구현

정점의 수가 작거나 간선의 수가 매우 많은 경우 우선순위 큐를 사용하지 않고 구현하는 방식이 빠른 경우가 있다.
다음 방문 정점을 큐에 보관하는 대신 매번 반복문을 이용해 방문하지 않는 정점 중 dist[]가 가장 작은 값을 찾는다.
방문해야 할 정점들의 목록을 저장하는 큐가 따로 없기 때문에, 각 정점을 방문했는지 여부는 별도의 visited[]를 통해 추적
이 경우 시간 복잡도: O(V^2 + E)

30.3, 30.4 신호 라우팅, ROUTING, 난이도: 하

간선 가중치의 합이 아니라 곱으로 정의된 문제
0이 아니라 1.0으로 초기화하면 된다.
log는 순증가 함수

30.5, 30.6 소방차, FIRETRUCKS, 난이도: 중

각 불난 위치에서 다익스트라, 각 소방서까지 거리 계산
각 소방서마다 다익스트라 실행, 각 불난 위치까지의 거리 계산
플로이드 알고리즘 사용해서 모든 쌍 거리 계산
3개 다 너무 시간이 오래 걸림

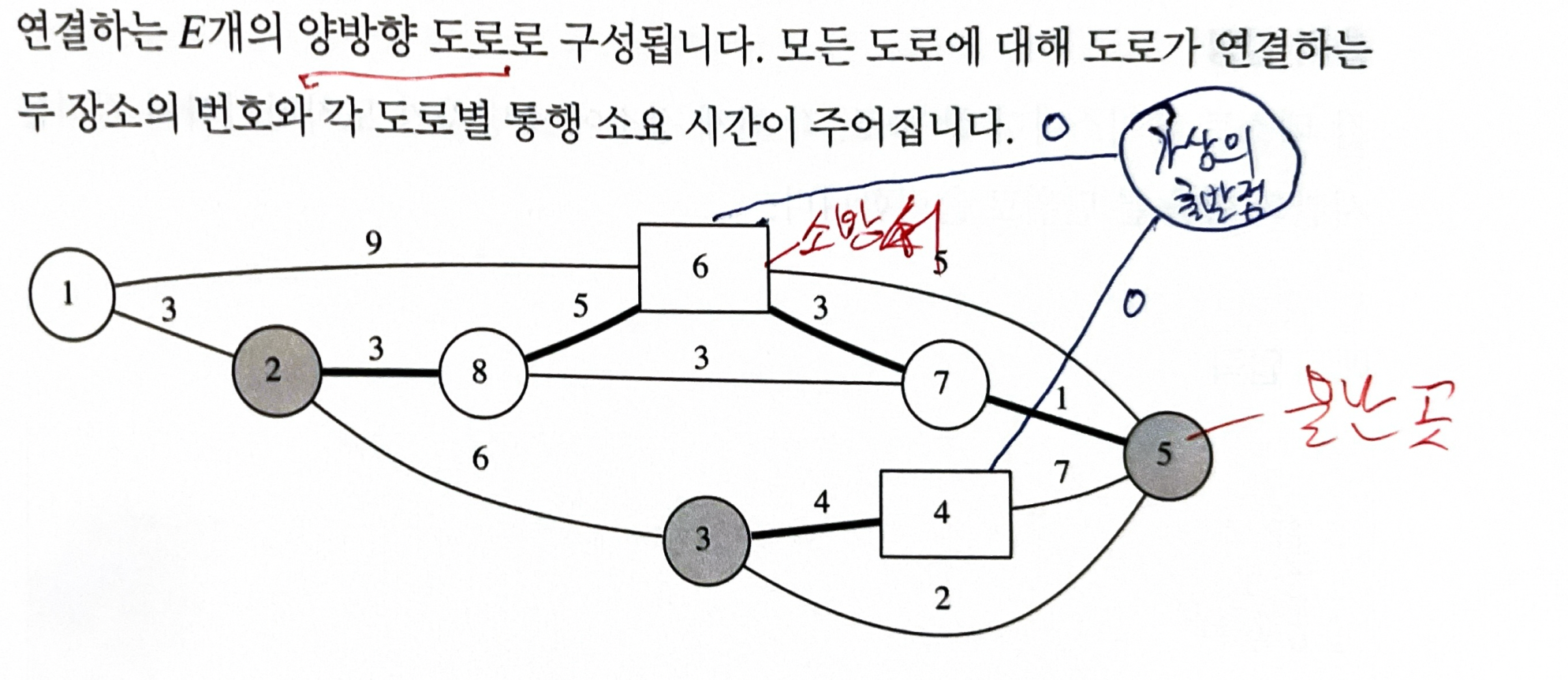
해법
- 각 소방서에서 다로 시작할 필요 없이 모든 소방서에서 동시에 다익스트라 수행하게 하자
- 가상의 시작점을 추가한뒤 이 시작점에서 다른 모든 소방서로 가중치 0인 간선을 연결
- 이 시작점에서 다익스트라 수행하면 모든 위치에 대해 가상의 소방서로 부터 최단 거리를 얻을 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def dijkstra(start):
    q = []
    heappush(q, (0, start))
    distance[start] = 0

    while q:
        cost, node = heappop(q)
        if distance[node] < cost:
            continue

        for (nxt, weight) in graph[node]:
            nxtCost = cost + weight
            if (nxtCost < distance[nxt]):
                distance[nxt] = nxtCost
                heappush(q, (nxtCost, nxt))

INF = float('inf')
for _ in range(int(input())):
    v, e, n, m = map(int, input().split())

    distance = [INF for _ in range(v + 1)]
    graph = [[] for _ in range(v + 1)]
    for _ in range(e):
        a, b, w = map(int, input().split())
        graph[a].append((b, w))
        graph[b].append((a, w))

    fires = list(map(int, input().split()))
    starts = list(map(int, input().split()))
    for i in starts:
        graph[0].append((i, 0))

    dijkstra(0)
    answer = 0
    for i in fires:
        answer += distance[i]
    print(answer)

30.9 벨만-포드 최단 경로 알고리즘

다익스트라와 같은 단일 시작점 최단 경로 알고리즘이지만, 음수 간선이 있어도 최단 경로를 찾을 수 있다.
그래프에 음수 사이클이 있어서 최단 거리가 제대로 정의되지 않을 경우, 이것에 대해 알려줌
시작점에서 각 정점까지 가는 최단 거리의 상한을 적당히 예측한 뒤, 예측 값과 실제 최단 거리 사이의 오차를 반복적으로 줄여가는 방식으로 동작
- BFS 기반으로 한 번에 하나씩 최단 거리를 확정해 나가는 다익스트라와 매우 다름
각 정점까지의 최단 거리의 상한을 담은 upper[] 1차원 배열을 유지
- 이 값은 알고리즘이 진행됨에 따라 점점 줄어들고, 종료될 때는 실제 최단 거리를 담게 된다.

30.9.1 벨만-포드 동작 과정

upper[start] = 0으로 초기화, 나머지 원소들은 INF로 초기화
최단 거리의 특성을 이용
- dist[v] <= dist[u] + w(u, v)
이 속성을 이용하면 upper 값을 실제 최단 거리에 가깝게 보정 가능
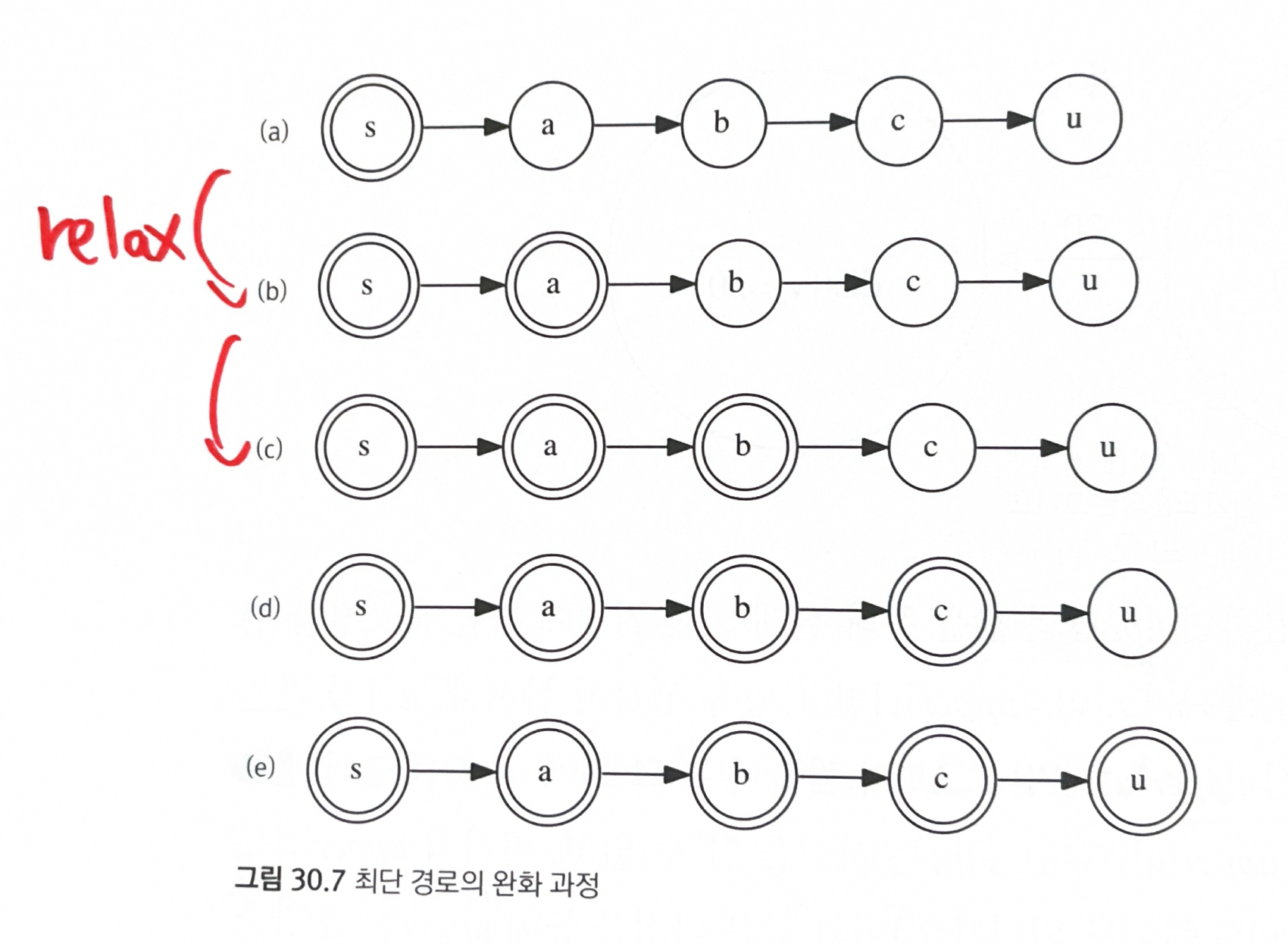
upper[v]를 감소하는 작업을 (u, v)를 따라 완화(relax) 한다고 말한다.
완화가 성공할때마다, upper는 줄어들고, 최단 거리에 가깝게 된다.

30.9.2 종료 조건과 정당성의 증명

upper[u] = dist[u]가 될 수 있나?
- 모든 간선에 대해 완화를 시도하는 작업을 x번 반복하면 x개 이하의 간선을 사용하는 최단 경로들은 전부 찾을 수 있다
- 모든 간선이 전부 완화가 실패할 때까지 반복하면 모든 최단 경로를 찾을 수 있다
몇 번 완화를 반복해야 하는가?
- 최단 경로가 한 정점을 두 번 지나는 일은 없기때문에, 최단 경로가 포함하는 간선 수의 상한은 쉽게 알 수 있다.
- 최단 경로는 최대 V개의 정점과 V-1 개의 간선을 가질 수 있다.
- 따라서, 완화는 전체 V-1번 이면 된다.

30.9.3 음수 사이클의 판정

음수 사이클이 있으면 최단 거리 문제가 제대로 정의 되지 않는다.
- 물론, 시잣점에서 음수 사이클로 가는 경로가 아예 없으면 상관 없다.
벨만-포드는 음수 사이클의 존재 여부를 판정할 수 있다.
- 의미 없는 값을 반환하는 대신 음수 사이클이 존재한다는 오류를 반환할 수 있다.
음수 사이클이 존재 여부를 판정하려면 V-1 번 완화가 아니라, V번 완화를 시도하면 된다.
- 그래프에 음수 사이클이 없다면 V-1번으로 모든 최단 거리를 찾을 수 있기 때문에, 마지막 반복의 완화는 전부 실패하게 된다.
- 음수 사이클이 있으면 V번째 반복에서도 항상 완화가 한 번은 성공한다.

30.9.4 실제 구현 (python 코드)

마지막 반복에서 완화가 성공하면(음수 사이클 존재) 텅 빈 배열을 반환
수행 시간은 모든 간선을 검사하는 중첩 반복문에 의 해 지배
- 가장 바깥의 for문은 V번
- 안의 두 for문은 모든 간선을 순회하므로 E번 수행
- 따라서, 전체 시간 복잡도는 O(VE) 이다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
V, E = map(int, input().split())
INF = float('inf')
graph = []
upper = [INF] * (V)
for i in range(E):
    s, e, w = map(int, input().split())
    graph.append((s, e, w))
mCycle = False

def bellmanFord():
    global mCycle
    upper[0] = 0
    for i in range(V - 1):  # V-1 번 반복
        updated = False
        for s, e, w in graph:
            if (upper[s] != INF) and (upper[e] > upper[s] + w):
                upper[e] = upper[s] + w
                updated = True
                
        if not updated: # 모든 간선에 대해 완화가 실패했을 경우 V-1번 돌 필요 없이 곧장 종료
            break

    for s, e, w in graph:  # 음수 사이클 판정
        if (upper[s] != INF) and (upper[e] > upper[s] + w):
            mCycle = True

if not mCycle:
    for i in range(1, V):
        if upper[i] != INF:
            print(upper[i])
        else:
            print(-1)
else:
    print(-1)

30.9.5 경로 계산하기

벨만-포드를 수행하는 과정에서 각 정점을 마지막으로 완화시킨 간선들을 모으면 스패닝 트리를 얻을 수 있다.
- 이 정점들은 항상 최단 경로 위에 있기 때문에, 각 정점에서부터 스패닝 트리의 루트인 시작점까지 거슬러 올라가는 경로는
- 항상 시작점에서 해단 경로까지의 최단 경로이다.
- BFS와 다익스트라와 같은 방식으로 실제 경로(정점의 목록)을 계산할 수 있다.

30.9.6 빠지기 쉬운 함정

u로 가는 경로가 존재하는지 확인하기 위해서는 적당히 큰 값 M에 대해 upper[u] < INF - M 인지를 확인해야 한다.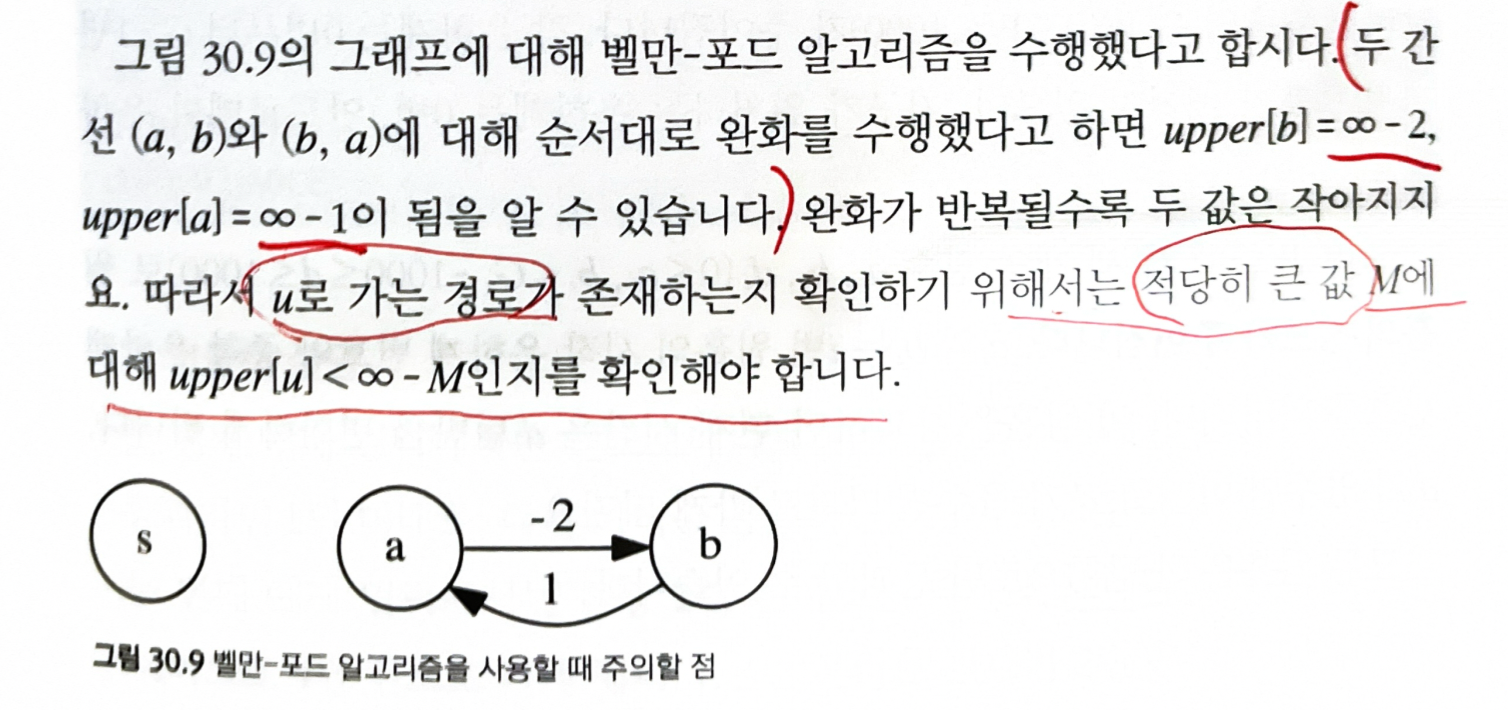

30.10, 30.11 시간여행, TIMETRIP, 난이도: 중

최단 경로 구하기
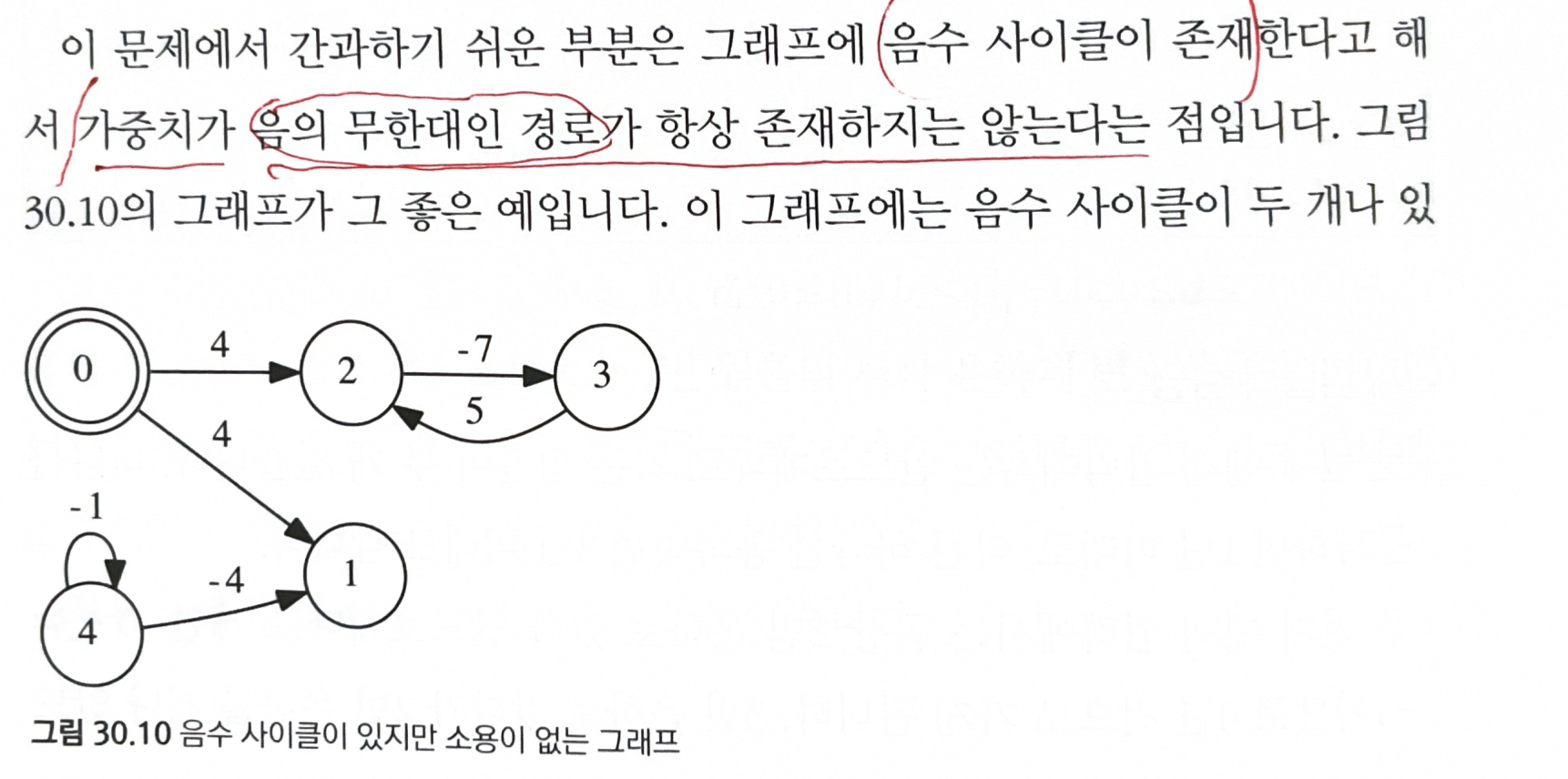
- 간과하기 쉬운 부분은 그래프에 음수 사이클이 존재한다고 해서, 가중치가 음의 무한대인 경로가 항상 존재하지는 않는다
- 음수 사이클을 발견했을 때 시작점에서 이 사이클로 왔다가 다시 종착점으로 가는 경로가 있는지 확인해야 한다.
- reachable[][]: 모든 정점의 쌍에 대해 한 정점에서 다른 정점으로 가는 경로의 존재 여부를 저장

최장 경로 구하기
- 주어진 그래프의 가중치의 부호를 모두 바꾼 다음 최단 경로를 찾으면 된다.
- 이 문제는 일반적으로 이야기하는 최장 경로 문제와는 다르다
- 이 문제와 달리 최장 경로 문제에서는 사이클을 포함하지 않는 단순 경로를 찾기 요구한다.
- 실제로 임의의 문제에서 단순 최장 경로를 찾는 문제는 NP-Complete 문제이다

30.12 플로이드의 모든 쌍 최단 거리 알고리즘

다익스트라, 벨만-포드는 one start node에서 다른 모든 정점까지의 거리를 구해준다.
- 물론, 각 정점을 시작점으로 다익스트라를 반복해도 모든 정점 쌍 최단 거리를 구할 수 있다.
플로이드는 모든 정점 쌍에 대해 둘 사이의 최단 거리를 구해준다.
2차원 배열 dist[]은 모든 정점 쌍의 최단 거리를 저장

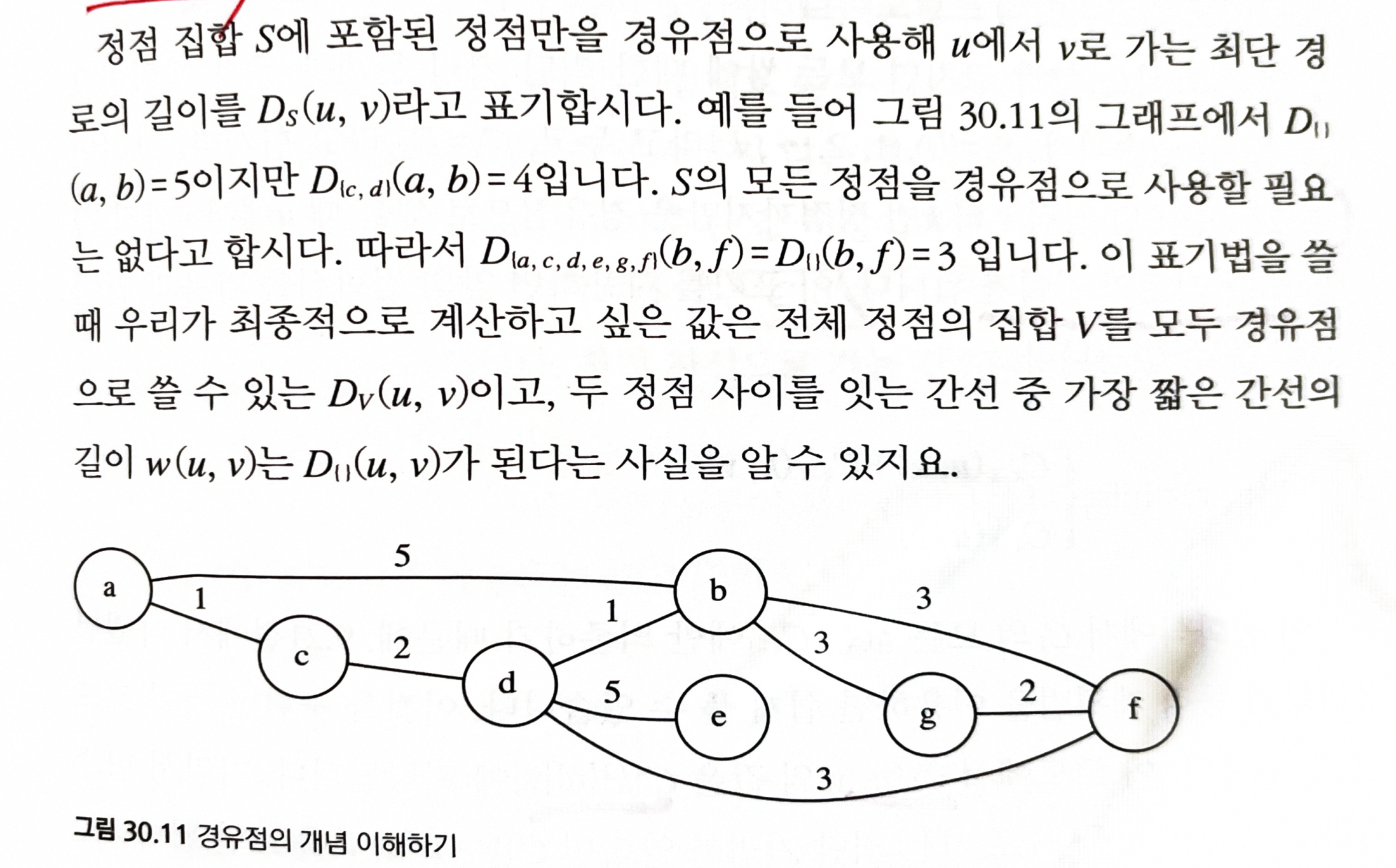
30.12.1 정점의 경유점

경유점: 경로가 거쳐가는 정점들
정점 집합 S에 포함된 정점들을 경유점으로 사용해 u -> v로 가는 최단 경로를 알고 있다고 할때, x 정점은 최단 경로를 경유하거나 경유하지 않는다.

경로가 x를 경유하지 않는다: 이 경로는 S - {x}에 포함된 정점들만을 경유점으로 사용
경로가 x를 경유한다: u->x 가는 구간과 x->v로 가는 구간으로 나눌 수 있다.

30.12.2 플로이드 알고리즘의 프로토타입

앞의 점화식을 고치면 모든 쌍에 대한 최단 거리 문제를 동적 계획법으로 풀 수 있다.
C k의 모든 값은 C k-1에만 의존하기 때문에, 동적 계획법을 이용하면 쉽게 풀 수 있다.
두 정점 사이의 간선이 없는 경우 아주 큰 값을 넣어 두면, 따로 처리하지 않아도 두 정점 사이의 경로가 존재하지 않은 것을 알 수 있다.
자기 자신으로 가는 간선은 따로 없더라도 최단 거리는 항상 0이기 때문에 C[0][u][u]는 0으로 초기화
전체 시간복잡도는 3중 for문이 지배, O(V^3)

30.12.3 메모리 사용량 줄이기

구현이 간단, 반복문 내부가 단순해서 빠르게 수행된다.
시간보다는 메모리 사용량이 문제가 된다.
슬라이딩 윈도우 기법을 사용하면 사용하는 배열의 크기를 O(V^2) 로 줄일 수 있다.
C k의 답은 C k-1만 있으면 계산할 수 있다.
- C k-2, C k-3 등은 가지고 있을 필요가 없다.
- C k(u, v)의 값을 C[k%2][u][v]에 저장한다.
별도의 배열을 사용하지 않고, 그래프의 가중치를 담는 인접 행렬 위에서 곧장 점화식의 결과를 계산
- C k-1 (u, k): 시작점 부터 k-1번 정점까지를 경유점으로 이용해 u -> k로 가는 최단 경로의 길이
- C k (u, k): 시작점 부터 k번 정점까지를 경유점으로 이용해 u -> k로 가는 최단 경로의 길이
- 출발점이나 도착점이 k일 때, 사용 가능한 경유점의 목록에 k가 추가되는 것은 의미가 없다.
  - ‘A를 들러 B에 가는 최단 경로’와
  - ‘A와 B를 들러 B로 가는 최단 경로’는 같다.
- Ck-1와 Ck의 값을 구분하지 않고 섞어서 써도 된다.
- C[k%2]와 C[(k-1)%2]를 구분할 필요가 없으며, 이들을 한 개의 2차원 배열에 섞어 써도 된다.
시간 복잡도: O(V^3), 그대로
공간 복잡도: O(V^2) 으로 줌

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
INF = float('inf')
graph = [[INF] * N for _ in range(N)]

for a in range(N):  # 자기 자신에서 자기 자신으로 가는 비용 0으로 초기화
    for b in range(N):
        if a == b:
            graph[a][b] = 0

for _ in range(M):  # 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
    a, b, c = map(int, input().split())
    graph[a][b] = c

for k in range(N):  # 점화식에 따라 플로이드 워셜 알고리즘을 수행
    for a in range(N):
        for b in range(N):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

30.12.4 실제 경로 계산하기

마지막으로 graph[u][v]을 갱신했을 때 사용한 k의 값을 저장 (따로 배열로 변수화 해서 저장)
- 이 정점의 번호를 w라고 하자
최단 경로가 w를 지난다는 의미
- 따라서, 재귀 호출을 이용해 u->w로 가는 최단 경로를 찾고, w-> v로 가는 최단 경로를 찾은 뒤 이 둘을 합친다.

Reference

프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 (구종만, 인사이트)
https://www.algospot.com/

30. 최단 경로 알고리즘#

30.1 도입#

30.1.1 음수 간선의 중요성#

30.1.2 단일 시작점과 모든 쌍 알고리즘#

30.1.3 방향 그래프와 무방향 그래프#

30.2 다익스트라의 최단 경로 알고리즘#

30.2.1 우선순위 큐를 사용하는 너비 우선 탐색#

30.2.2 실제 구현 (python 코드)#

30.2.3 다익스트라 시간 복잡도#

30.2.4 실제 경로 찾기#

30.2.5 O(VlgV)에 다익스트라 구현하기#

30.2.6 우선순위 큐를 사용하지 않는 다익스트라의 구현#

30.3, 30.4 신호 라우팅, ROUTING, 난이도: 하#

30.5, 30.6 소방차, FIRETRUCKS, 난이도: 중#

30.9 벨만-포드 최단 경로 알고리즘#

30.9.1 벨만-포드 동작 과정#

30.9.2 종료 조건과 정당성의 증명#

30.9.3 음수 사이클의 판정#

30.9.4 실제 구현 (python 코드)#

30.9.5 경로 계산하기#

30.9.6 빠지기 쉬운 함정#

30.10, 30.11 시간여행, TIMETRIP, 난이도: 중#

30.12 플로이드의 모든 쌍 최단 거리 알고리즘#

30.12.1 정점의 경유점#

30.12.2 플로이드 알고리즘의 프로토타입#

30.12.3 메모리 사용량 줄이기#

30.12.4 실제 경로 계산하기#

Reference#

30. 최단 경로 알고리즘

30.1 도입

30.1.1 음수 간선의 중요성

30.1.2 단일 시작점과 모든 쌍 알고리즘

30.1.3 방향 그래프와 무방향 그래프

30.2 다익스트라의 최단 경로 알고리즘

30.2.1 우선순위 큐를 사용하는 너비 우선 탐색

30.2.2 실제 구현 (python 코드)

30.2.3 다익스트라 시간 복잡도

30.2.4 실제 경로 찾기

30.2.5 O(VlgV)에 다익스트라 구현하기

30.2.6 우선순위 큐를 사용하지 않는 다익스트라의 구현

30.3, 30.4 신호 라우팅, ROUTING, 난이도: 하

30.5, 30.6 소방차, FIRETRUCKS, 난이도: 중

30.9 벨만-포드 최단 경로 알고리즘

30.9.1 벨만-포드 동작 과정

30.9.2 종료 조건과 정당성의 증명

30.9.3 음수 사이클의 판정

30.9.4 실제 구현 (python 코드)

30.9.5 경로 계산하기

30.9.6 빠지기 쉬운 함정

30.10, 30.11 시간여행, TIMETRIP, 난이도: 중

30.12 플로이드의 모든 쌍 최단 거리 알고리즘

30.12.1 정점의 경유점

30.12.2 플로이드 알고리즘의 프로토타입

30.12.3 메모리 사용량 줄이기

30.12.4 실제 경로 계산하기

Reference