31. 최소 스패닝 트리

31.1 도입

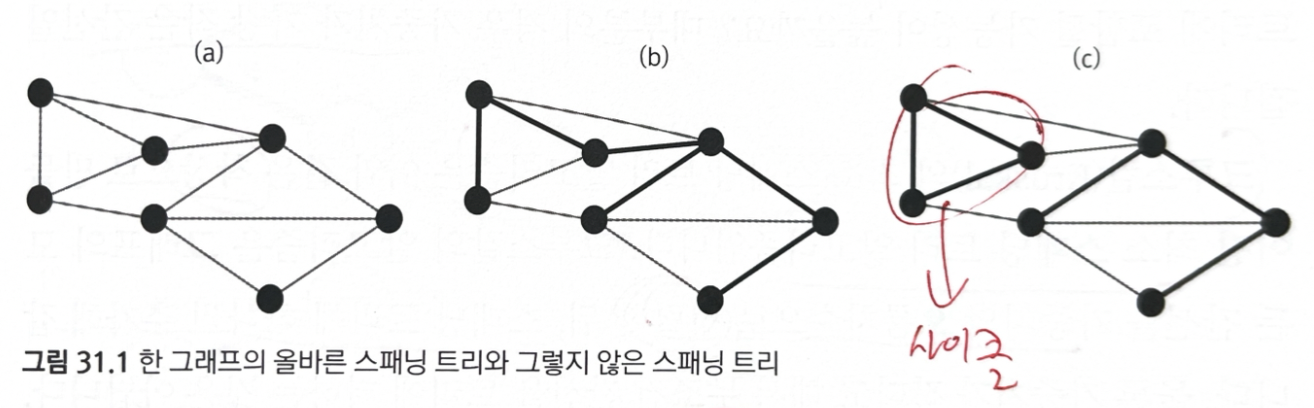
  • 스패닝 트리: 원래 그래프의 정점 전부와 간선의 부분 집합으로 구선된 부분 그래프

    • 트리 형태로 전부 연결해야 한다.
    • 간선들이 사이클을 이루지 않는다
    • 정점들이 부모-자식 관계로서 연결될 필요는 없다
    • 그래프의 스패닝 트리는 유일하지 않다. 여러개 가능

  • 최소 스패닝 트리(MST): 스패닝 트리 중 가중치의 합이 가장 작은 트리

    • 그래프의 연결성을 그대로 유지하는 가장 저렴한 그래프를 찾는 문제

  • N개의 정점이 있으면 MST를 구성하는 간선의 개수는 항상 N - 1 개다.

  • 최소 스패닝 트리을 찾는 크루스칼, 프림 알고리즘 모두 탐욕적(Greedy) 알고리즘

image-20240425200125668.png

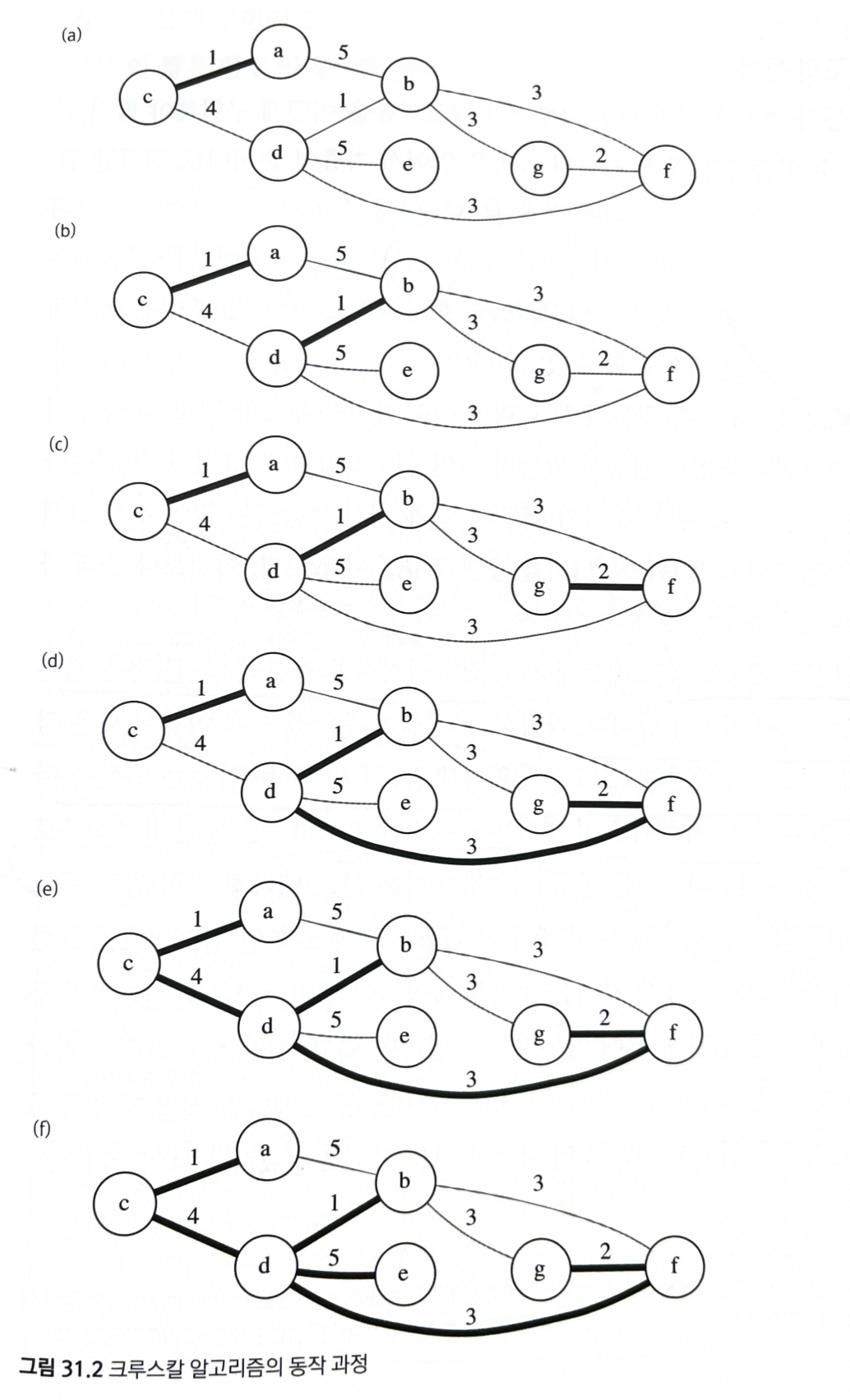
31.2 크루스칼의 최소 스패닝 트리

  • 가중치가 가장 작은 간선과 가장 큰 간선 중 어느 쪽이 최소 스패닝 트리에 포함될 가능성이 높을까?
    • 대부분의 경우 가중치가 가장 작은 간선이다.
    • 이 아이디어에 착안한 알고리즘
  • 간선을 가중치의 오름차순으로 정렬, 스패닝 트리에 하나씩 추가
  • 물론, 가중치가 작다고 해서 무조건 간선에 추가하는 것은 아니다.
    • 사이클이 생길 수 있기 때문이다.
    • 사이클이 생기는 간선은 고려에서 제외해야 함.
  • 모든 간선을 한 번씩 검사하고 나서 종료

image-20240425200144524.png

31.2.1 자료구조의 선택

  • 어떻게 사이클 판별을 효율적으로 할 것인가?
    • 간선을 추가해서, 그래프에 사이클이 생기려면 간선의 양 끝점은 같은 컴포넌트에 속해 있어야 한다.
    • 두 정점이 주어졌을 때, 이들이 같은 컴포넌트에 속하는지 확인하고, 그렇지 않다면 두 컴포넌트를 합치는 연산을 빠르게 한다.
    • 여기서, 상호 배타적 집합 자료 구조, Union-find 가 사용된다.
      • 이 자료구조에서 한 집합은 그래프의 한 컴포넌트를 표현한다.
    • 새 간선을 추가해 사이클이 생기는지 확인하려면, 두 정점이 이미 같은 집합에 속해 있는지 확인하면 된다.
    • 간선을 트리에 추가할 경우에는 이들이 포함된 두 집합을 합친다.

31.2.2 구현 (python 코드)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

from heapq import *

def find(a):
    if a == parent[a]: return a
    else:
        parent[a] = find(parent[a])
        return parent[a]

def union(a, b):
    a, b = find(a), find(b)
    if a != b: parent[b] = a

N, M = map(int, input().split())
parent, h = [0] * N, []
useEdge, totalCost = 0, 0
for i in range(N): parent[i] = i

for i in range(M):
    s, e, w = map(int, input().split())
    heappush(h, (w, s, e))  # (weight, start, end), 제일 앞 순서로 정렬되므로, 가중치를 제일 앞 순서로 함.

while h:
    w, s, e = heappop(h)
    if find(s) != find(e):  # find 연산 후, 부모노드 다르면 사이클 발생 X으므로 union 연산 수행 -> 최소 신장 트리에 포함!
        union(s, e)
        totalCost += w
        useEdge += 1

print(totalCost)
  • 여기서, 상호 배타적 집합 자료 구조, Union-find 의 연산은 상수 시간 이 걸린다.
  • 실제 트리를 만드는 for문의 시간 복잡도는 O(E)
  • 전체 시간 복잡도는 간선 목록의 정렬에 걸리는 O(E lgE)

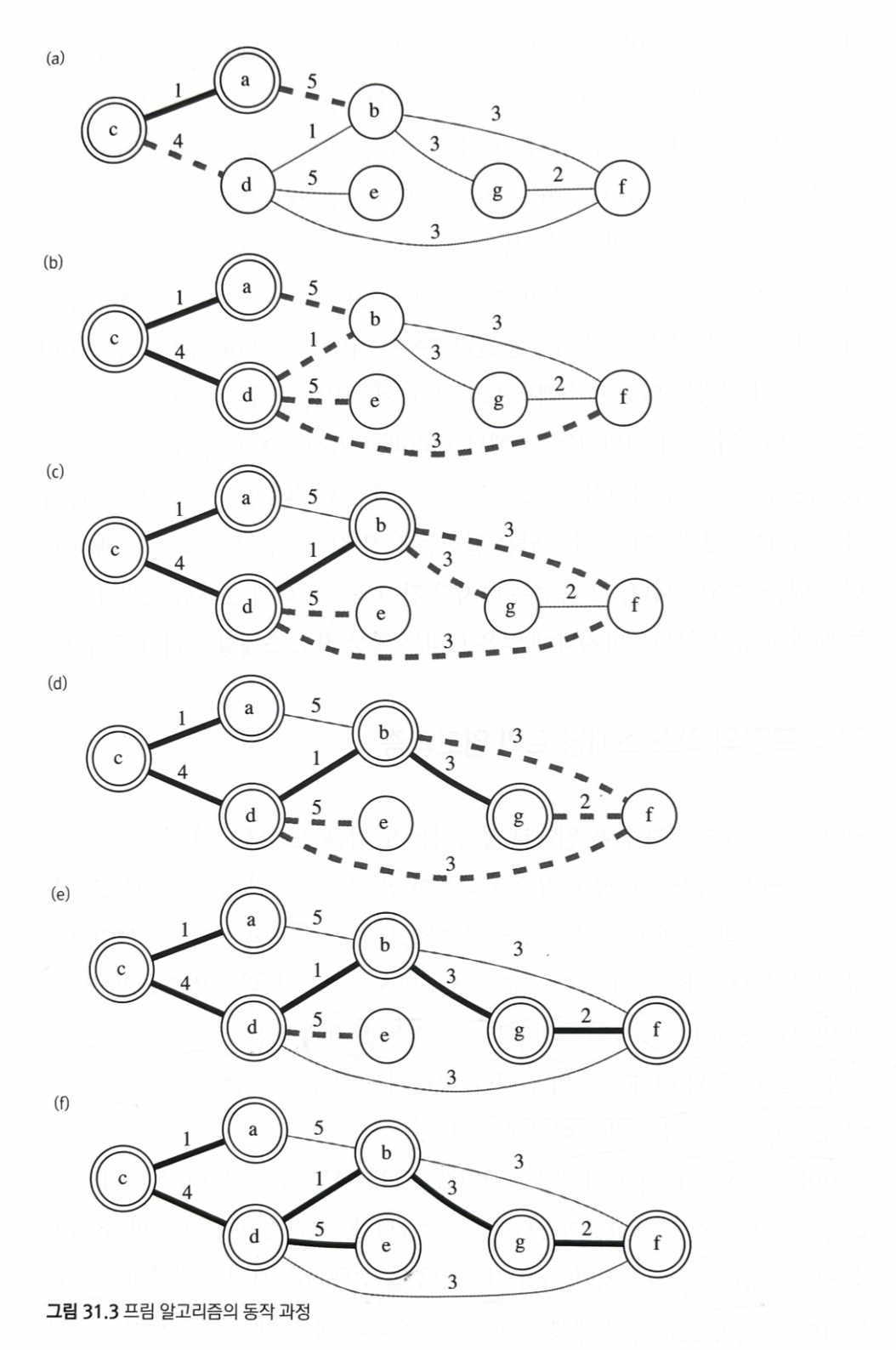
31.3 프림의 최소 스패닝 트리

  • 다익스트라와 비슷

  • 하나의 시작점으로 구성된 트리에, 간선을 하나씩 추가하며 스패닝 트리가 될 때까지 키워 간다.

    • 중간 과정에서도 항상 연결된 트리를 이루게 된다.

  • 크루스칼 알고리즘과 똑같이, 가중치가 가장 작은 간선을 선택한다.

image-20240425200155842.png

31.3.1 구현 (python 코드), 우선순위 큐 사용

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

from heapq import *

def prim(graph):
    result, vi, start, h = [], set(), list(graph.keys())[0], []
    vi.add(start)
    for end, cost in graph[start].items():
        heappush(h, (cost, start, end))

    while h:
        cost, s, e = heappop(h)
        if e not in vi:
            vi.add(e)
            result.append((s, e, cost))
            for nxtNode, nCost in graph[e].items():
                if nxtNode not in vi:
                    heappush(h, (nCost, e, nxtNode))

    return result

prim(graph={
    'A': {'B': 7, 'D': 5},
    'B': {'A': 7, 'C': 8, 'D': 9, 'E': 7},
    'C': {'B': 8, 'E': 5},
    'D': {'A': 5, 'B': 9, 'E': 15, 'F': 6},
    'E': {'B': 7, 'C': 5, 'D': 15, 'F': 8, 'G': 9},
    'F': {'D': 6, 'E': 8, 'G': 11},
    'G': {'E': 9, 'F': 11}
})
  • 다익스트라 알고리즘 처럼 우선순위 큐(heap) 을 사용해서 구현하면 O(ElgV) 의 시간 이 걸린다.
  • 우선순위 큐를 사용하지 않은 경우는 O(V^2 + E)
    • 밀집 그래프의 경우 V^2 === E 임으로, 프림 알고리즘이 크루스칼 알고리즘 보다 빠르다.

Reference