1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

from collections import deque

# graph는 그래프. 간선의 비용 정보
# s는 시작 노드, t는 도착 노드, n은 노드의 개수
def fordFulkerson(graph, start, target, n):
    remain = [[0] * n for _ in range(n)]
    for i in range(n):
        for j in range(n):
            remain[i][j] = graph[i][j]

    maxFlow = 0  # 최대 유량
    while True:  # bfs
        visited = [False] * n
        visited[start] = True
        queue = deque([start])
        path = [-1] * n  # 경로. 부모 노드를 저장. 거슬러 올라가면 경로 구할 수 있음
        path[start] = -1  # 처음 노드는 부모 노드가 없음

        while queue:
            a = queue.popleft()
            for b in range(n):
                if not visited[b] and remain[a][b] > 0:  # 방문하지 않았고 갈 수 있다면
                    queue.append(b)
                    path[b] = a  # 부모 노드 저장
                    visited[b] = True

        if not visited[target]:  # 목적지로 가는 경로가 없다면
            break  # bfs 끝. 경로는 도착 노드인 t 부터 path를 보면서 부모 노드를 거슬러 올라가면 됨

        b = target  # 경로를 거슬러 올라가기 위한 변수
        min_remain = float('inf')  # 경로 간선들 중 가장 작은 용량을 구하기 위한 변수
        while b != start:  # 처음 노드에 도착할 때까지
            a = path[b]
            min_remain = min(min_remain, remain[a][b])
            b = a

        b = target
        while b != start:
            a = path[b]
            remain[a][b] -= min_remain
            remain[b][a] += min_remain
            b = a
        maxFlow += min_remain

    return maxFlow

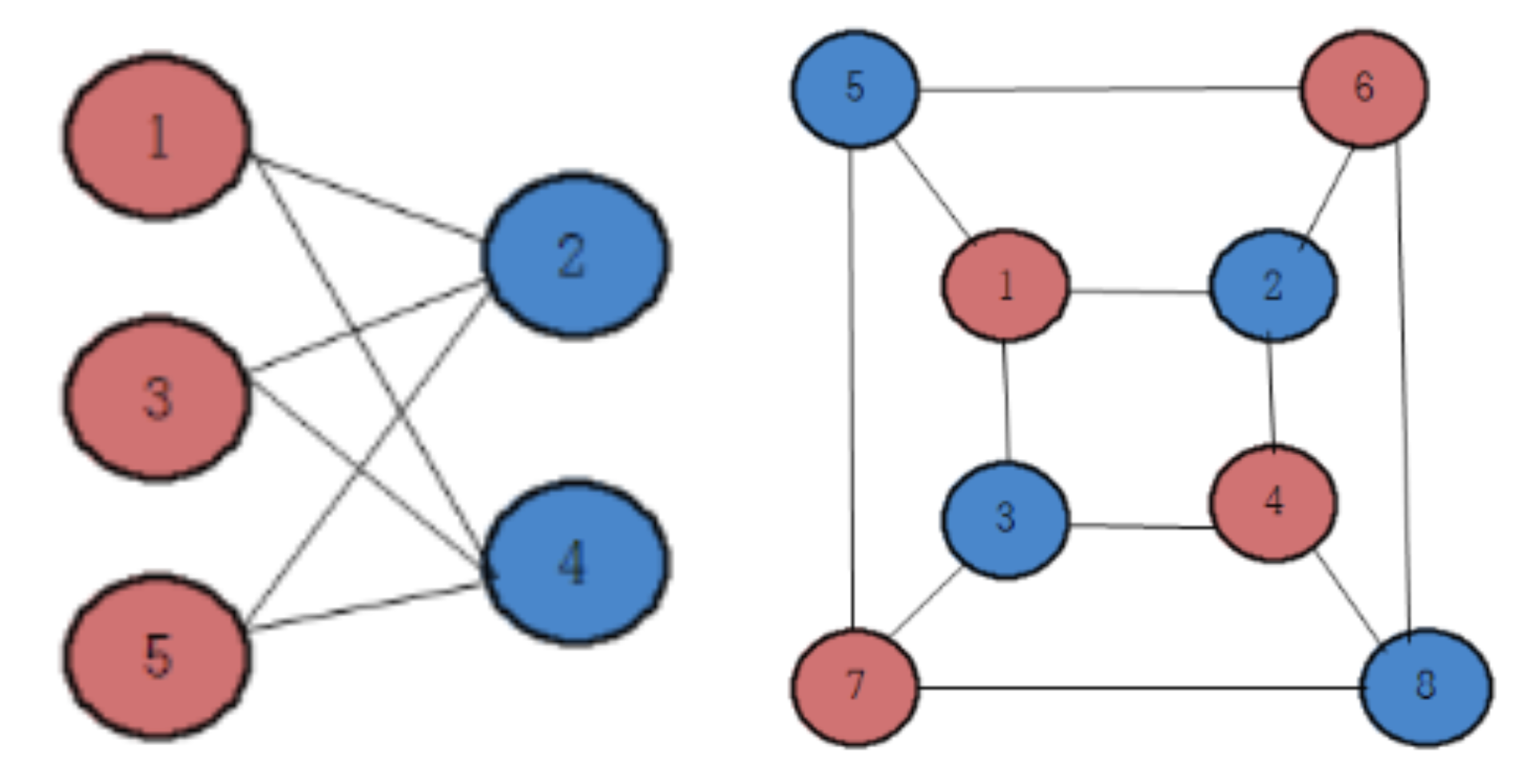
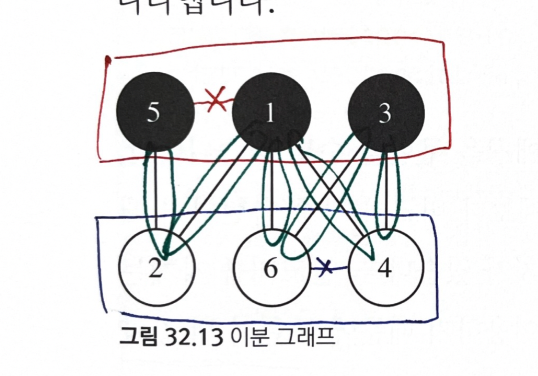
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

from collections import deque

def odd_even(n):
    return 1 if n % 2 == 0 else -1

def bfs(current):
    level = 0
    queue = deque([(current, level + 1)])
    vi[current] = odd_even(level)  # 깊이에 따라, 서로 다른 색상을 칠해준다. (인접한 정점 끼리는 같은 색상)

    while queue:
        now = queue.popleft()
        curNode, level = now

        for nxt in graph[curNode]:
            if not vi[nxt]:  # 방문한 적이 없다면 두 색상 중 하나로 칠해준다.
                queue.append((nxt, level + 1))
                vi[nxt] = odd_even(level)
            elif vi[nxt] == odd_even(level):  # 방문한 적이 있고, 현재 칠하려는 색상과 같으면 pass
                continue
            elif vi[nxt] != odd_even(level):  # 방문한 적이 있고, 현재 칠하려는 색상과 다르다면, 인접리스트가 아니다.
                return False

    return True

result = []
vertex, edge = map(int, input().split())
graph = [[] for _ in range(vertex)]
vi = [0] * (vertex)
for _ in range(edge):
    u, v = map(int, input().split())
    graph[u].append(v)
    graph[v].append(u)

graph_list = []  # 그래프의 정점이 서로 이어지지 않았을 수 있음 (두개의 그래프 존재 가능성)
for i in range(vertex):
    if not vi[i]:
        graph_list.append(bfs(i))

print(*result)